НЕУСТОЙЧИВОСТЬ ГРАВИТАЦИОННОЙ ПОСТОЯННОЙ

НЕУСТОЙЧИВОСТЬ ГРАВИТАЦИОННОЙ ПОСТОЯННОЙ

Гравитационная постоянная (G) впервые появилась в выведенном Ньютоном уравнении силы тяжести, в соответствии с которым сила гравитационного взаимодействия двух тел равна отношению умноженного на нее произведения масс этих взаимодействующих тел к квадрату расстояния между ними. Значение этой константы многократно измерялось с тех пор, как в 1798 г. было впервые определено в точном эксперименте Генри Кавендишем. «Лучшие» результаты измерений за последние 100 лет отображены на ил. 13.

В начальной стадии измерений наблюдался значительный разброс результатов, а затем прослеживается хорошая сходимость получаемых данных. Тем не менее даже после 1970 г. «лучшие» результаты колеблются в диапазоне от 6,6699 до 6,6745, то есть разброс составляет 0,07 %.[238] (Единицы, в которых выражается значение гравитационной постоянной, имеют вид ?10–11 м3 кг-1с-2.)

Из всех известных фундаментальных констант именно численное значение гравитационной постоянной определено с наименьшей точностью, хотя важность этой величины трудно переоценить. Все попытки прояснить точное значение этой константы не увенчались успехом, а все измерения так и остались в слишком большом диапазоне возможных значений. Тот факт, что точность численного значения гравитационной постоянной до сих пор не превышает 1/5000, редактор журнала «Нейчур» определил как «пятно позора на лице физики».[239] В последние годы неопределенность действительно была так велика, что для объяснения гравитационных аномалий даже вводились совершенно новые силы.

В начале 80-х гг. Фрэнк Стейси со своими коллегами измерял эту константу в глубоких шахтах и скважинах Австралии, и полученное им значение оказалось примерно на 1 % выше официального значения, принятого в настоящее время. Например, в серии экспериментов, проведенных в Квинсленде, в шахте Хилтон, было обнаружено, что значение гравитационной постоянной находится в пределах 6,734 ± 0,002, в то время как официально признанное значение составляет 6,672 ± 0,003.[240] Результаты исследователей в Австралии были воспроизводимы и хорошо согласовывались друг с другом,[241] но вплоть до 1986 г. на них практически не обращали внимания.

Затем Эфрейн Фишбах из университета Вашингтона (Сиэтл) вызвал шок среди ученых, заявив, что его лабораторные измерения также показали небольшое отклонение от закона всемирного тяготения по Ньютону, причем полученные результаты хорошо согласовывались с данными австралийских ученых. Фишбах провел повторный анализ результатов, в 20-е гг. полученных Роландом Эотвесом и всегда считавшихся наглядным примером точных измерений. Он обнаружил, что в классических опытах отмечалась аналогичная аномалия в некоторых данных, которые затем были сочтены случайной ошибкой.[242] На основе этих лабораторных испытаний и наблюдений в австралийских шахтах Фишбах предположил, что существует до тех пор неизвестная сила отталкивания, так называемая «пятая сила» (четырьмя известными взаимодействиями были сильное, слабое, электромагнитное и гравитационное).

Дальнейшие тщательные измерения гравитационной постоянной, которые проводились в сверхглубоких скважинах, пробуренных в арктической полярной шапке, а также на значительных высотах, представили дополнительные свидетельства существования «пятой силы».[243]

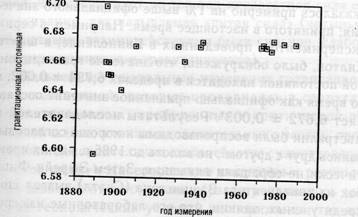
Ил. 13. Лучшие измерения значения гравитационной постоянной (G) с 1888 по 1989 гг.

Интерпретация полученных результатов зависела от того, каким образом учитывалось влияние геологических условий эксперимента, так как плотность окружающих скал воздействовала на измеряемую величину силы тяжести. Экспериментаторы были хорошо осведомлены об этом обстоятельстве и ввели в свои измерения соответствующие поправки. Скептики тем не менее утверждали, что поблизости могли находиться не учтенные экспериментаторами скалы необычайно высокой плотности, и необычную величину гравитационной постоянной определило именно воздействие этих скальных пород.[244] До настоящего времени такая точка зрения преобладает, хотя вопрос о существовании «пятой силы» по-прежнему открыт. Эта тема остается предметом теоретических и экспериментальных изысканий.[245]

Возможное существование «пятой силы» практически не влияет на изменения гравитационной постоянной во времени. Однако сам факт, что в конце двадцатого столетия серьезно обсуждался вопрос о некой дополнительной силе, воздействующей на гравитацию, свидетельствует о том, что теория гравитации не слишком продвинулась вперед за три столетия после публикации «Начала» Ньютона.

Предположение Поля Дирака и других физиков-теоретиков о том, что гравитационная постоянная может уменьшаться по мере расширения Вселенной, было воспринято некоторыми специалистами в метрологии достаточно серьезно. Однако предполагаемое Дираком изменение было весьма незначительным — приблизительно 5/(1011) в год. Такое изменение нельзя подтвердить существующими на сегодняшний день методами проводимых на Земле измерений, так как «лучшие» результаты, полученные за последние двадцать лет, отличаются друг от друга более чем на 0,0005. Иными словами, предполагаемое изменение меньше разницы в существующих «лучших» результатах примерно в десять миллионов раз.

Для проверки предложенной Дираком гипотезы были опробованы различные косвенные методы. Одни из этих методов основывались на геологических данных — к примеру, на измерении угла наклона ископаемых песчаных дюн, по которому можно было вычислить силу тяжести, воздействующую в период образования этих дюн. В других методах использовались данные о затмениях за последние 3000 лет. При некоторых способах проверки применялись новейшие астрономические методы. В ходе одного из экспериментов, проводимых в рамках космической программы, через равные промежутки времени измерялось расстояние до Луны. При этом использовался радар усложненной конструкции, которая позволила установить решетку с отражателями прямо на лунную поверхность. Время прохождения лазерных импульсов — от момента пуска до регистрации телескопом — измерялось через равные промежутки времени. Более точный эксперимент с использованием радара удалось провести благодаря полету «Викинга» к Марсу: импульсы к Земле посылались с поверхности Марса спускаемым аппаратом. Эти измерения продолжались с 1976 по 1982 гг. Если предположить, что скорость света в вакууме остается постоянной, радарные методы позволяют определять расстояние от Марса до Земли с точностью в несколько метров. Полученные данные вводились в сложные математические модели орбит различных тел в Солнечной системе, в результате чего уточнялось их соответствие установленному значению гравитационной постоянной. Однако такие вычисления допускали множество неопределенностей, включая предположения о воздействии на орбиту Марса крупных астероидов с неизвестной массой. Один вариант вычислений дал результаты, подтверждающие изменения гравитационной постоянной на 0,2/(1011) в год.[246] Другой метод вычислений, в котором использовались те же самые данные, дал результат, на порядок превышавший предыдущий, но и он был ниже 1/(1010) в год.[247]

Еще один астрономический метод заключался в изучении динамики расстояния между объектами в двойном пульсаре. Уточнялось, действительно ли гравитационная постоянная за время наблюдений сохраняет неизменную величину. Но и в этом случае при вычислениях использовалось слишком много предположений, что делает результаты исследования недостоверными для любого, кто захотел бы повторить эксперимент, изменив принятые допущения.[248]

Некоторые физики считают, что по крайней мере часть имеющихся данных указывает на незначительные изменения гравитационной постоянной во времени.[249] На основе данных, полученных в экспериментах с Луной, часть ученых пришла к заключению, что гравитационная постоянная может меняться по меньшей мере в такой степени, как предполагал Дирак,[250] однако другие с этим не согласны.[251] Патриарх британской метрологии Брайан Петли интерпретировал все эти исследования следующим образом:

«Если считать достоверными космологические измерения времени и полагать, что мы обладаем достаточным пониманием гравитации, то изменения гравитационной постоянной составят менее 1/иок>) в год. Этот вывод подтверждается рядом различных доказательств, часть которых получена в кратковременных экспериментах. Если считать изменения, предсказанные Дираком, неверными, остается признать, что флуктуации значений гравитационной постоянной либо зависят от времени в крайне незначительной степени, либо имеют циклический характер, причем в настоящее время эти изменения особенно незначительны».[252]

Со всеми этими косвенными доказательствами проблема в том, что все они зависят от сложной цепи теоретических предположений, включая гипотезу о постоянстве других физических констант. Они остаются убедительными только в рамках принятой системы воззрений. Если считать достоверными современные космологические теории, сами по себе предполагающие неизменность гравитационной постоянной G, то данные становятся внутренне согласованными только при условии, что все изменения от эксперимента к эксперименту или от метода к методу мы будем считать результатом ошибки.