Глава вторая Об отражении

Глава вторая

Об отражении

Объяснив явления световых волн, распространяющихся в однородной среде, мы исследуем затем, что происходит с ними при встрече с другими телами. Сперва мы покажем, как этими же волнами объясняется отражение света и почему при нем сохраняется равенство углов.

Пусть АВ (рис. 56) будет плоская и полированная поверхность какого-нибудь металла, стекла или другого тела, которую я сначала приму за совершенно гладкую (о неровностях, от которых она не может быть свободна, я скажу позднее), и пусть прямая AC, наклонная к АВ, представляет собой часть световой волны, центр которой будет так далеко, что эта часть AC может быть принята за прямую линию. Я рассматриваю все это как бы в одной плоскости, представляя себе, что плоскость, в которой находится это изображение, пересекает сферу волны через ее центр, а плоскость АВ – под прямыми углами, о чем достаточно предупредить раз навсегда.

Точка С волны AC в некоторый промежуток времени продвинется до плоскости АВ к точке В по прямой СВ, которую должно представлять себе исходящей из светящегося центра и которая, следовательно, перпендикулярна к AC. Но за тот же промежуток времени точка той же волны А не могла – по крайней мере, отчасти – сообщить свое движение за пределы плоскости АВ и должна была продолжить свое движение в материи, находящейся над этой плоскостью, притом на протяжении, равном СВ; вместе с тем она должна была, согласно сказанному выше, образовать свою отдельную сферическую волну. Указанная волна изображена здесь окружностью SNR, центр которой в А, а полудиаметр AN равен СВ.

Если затем рассмотреть остальные точки H волны AC, то ясно, что они не только достигнут поверхности АВ по прямым НК, параллельным СВ, но еще породят в прозрачной среде из центров К отдельные сферические волны, представленные тут окружностями, полудиаметры которых равны линиям КМ, т. е. продолжениям линий НК до прямой BG, параллельной AC.

Но все эти окружности, как это легко видеть, имеют общей касательной прямую BN, т. е. ту же прямую, которая является касательной из точки В к первому из этих кругов, центром которого была точка А, а полудиаметром, равным прямой ВС, AN.

Итак, прямая BN (заключенная между точками В и N, на которую падает перпендикуляр из точки А) как бы образована всеми этими окружностями и заканчивает движение, возникшее при отражении волны AC; в этом месте поэтому движение имеется в гораздо большем количестве, чем где-либо. Поэтому, согласно объясненному выше, BN является распространением волны AC в тот момент, когда ее точка С достигла точки В. Действительно, нет другой прямой, которая, как BN, была бы общей касательной всех данных кругов, если не считать BG под плоскостью АВ; эта BG была бы продолжением волны, если бы движение могло распространяться в среде, однородной с той, которая находится над плоскостью. Если мы хотим видеть, как волна AC постепенно достигла BN, то достаточно провести в той же фигуре прямые КО, параллельные BN, и прямые KL, параллельные AC. Тогда мы увидим, что волна AC из прямой последовательно становится ломаной во всех положениях OKL и снова становится прямой в NB.

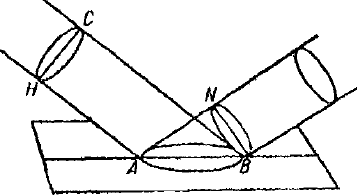
Рис. 57

Но отсюда видно, что угол отражения оказывается равным углу падения. <….>

Рассматривая предшествующее доказательство, можно было бы сказать, что хотя BN действительно является общей касательной всех круговых волн в плоскости этого рисунка, но что эти волны, будучи на самом деле сферическими, имеют, кроме того, еще бесконечное число подобных касательных, которыми будут все прямые, проведенные из точки В по поверхности конуса, образуемого прямою BN при вращении вокруг оси BA. Остается, следовательно, показать, что в этом обстоятельстве не имеется никакой трудности; заодно выяснится, почему падающий и отраженный лучи находятся всегда в одной и той же плоскости, перпендикулярной к отражающей плоскости. И вот я говорю, что волна AC, рассматриваемая только как линия, не производит света. Дело в том, что видимый световой луч, как бы он ни был узок, всегда имеет некоторую толщину; поэтому, чтобы представить волну, продвижение которой производит этот луч, нужно вместо линии AC взять плоскую фигуру, подобно кругу HC на данном рисунке (рис. 57), предполагая, как было сделано раньше, что светящаяся точка бесконечно удалена. Но из предшествующего доказательства легко видеть, что каждая маленькая точка этой волны HC, достигнув плоскости АВ, породит там свою отдельную волну, и все эти волны, когда точка С достигнет точки В, будут иметь общую касательную плоскость, а именно круг BN, равный СН; этот круг будет пересечен посредине под прямыми углами той же самой плоскостью, которая таким же образом пересекает круг СН и эллипс АВ. Также видно, что указанные сферы отдельных волн не могут иметь другой общей касательной плоскости, кроме круга BN; в этой плоскости отраженного движения будет гораздо больше, чем где-либо в другом месте, и поэтому она будет нести в себе свет, являющийся продолжением волны СН.

Я утверждал в предшествующем доказательстве, что движение точки А падающей волны не может, по крайней мере полностью, передаться за плоскость АВ. Здесь надо заметить, что хотя движение эфирной материи и передалось частью материи отражающего тела, но это ни в чем не может изменить скорость продвижения волны, от которой зависит угол отражения. В самом деле, в одном и том же веществе легкий удар должен вызвать столь же скорые волны, как и очень сильный удар. Это зависит от одного свойства обладающих упругостью тел, а именно: что и слабо и сильно сжатые тела восстанавливают свою форму в одинаковое время. Следовательно, при всяком отражении света от какого бы то ни было тела углы падения и отражения должны быть равными, хотя бы даже это тело и обладало свойством отнимать часть движения, производимого падающим светом. И опыт показывает, что, действительно, нет ни одного полированного тела, отражение от которого не следует этому правилу.

В нашем доказательстве надо в особенности подчеркнуть, что оно не требует, чтобы отражающая поверхность рассматривалась как совершенно ровная плоскость, как то предполагали все те, которые старались объяснить явления отражения; эта поверхность должна быть только настолько ровной, насколько это возможно при образовании ее частицами материи отражающего тела, помещенными одна около другой. Эти частицы больше частиц эфирной материи, как будет ясно из того, что мы скажем при рассмотрении прозрачности и непрозрачности тел. Действительно, так как поверхность, таким образом, будет состоять из расположенных рядом частиц, а эфирные частицы будут сверху и они будут меньше, то ясно, что нельзя доказать равенства углов падения и отражения сходством с тем, что происходит с мячом, брошенным в стену, – сходством, которым всегда пользовались.

Между тем по нашему способу дело объясняется просто. Так как малость частиц, например ртути, такова, что на самой маленькой данной видимой поверхности их нужно представить себе миллионы, то, если эти частицы расположены наподобие кучи песку, которую разровняли настолько, насколько это можно сделать, эта поверхность будет, по нашему мнению, такой же ровной, как полированное стекло; и хотя она всегда остается шероховатой относительно частиц эфира, но ясно, что центры всех отдельных сфер отражения, о которых мы говорили, находятся приблизительно в одной и той же ровной плоскости и что, таким образом, их общая касательная плоскость в достаточной степени соответствует тому, что требуется для получения света. А только это и требуется для доказательства по нашему способу равенства названных углов; остальное отражаемое отовсюду движение не может вызвать какого-либо противоположного действия.

Данный текст является ознакомительным фрагментом.