Нейтральные мутации и генетический дрейф — движение без правил
Нейтральные мутации и генетический дрейф — движение без правил
Ландшафт приспособленности — образ яркий и полезный, но, как и всякая модель, он несовершенен. Многие аспекты эволюционного процесса с его помощью отразить трудно или невозможно. Реальный ландшафт приспособленности переменчив (впрочем, как и реальные горные системы). Если один белок в клетке изменился, это хоть немного, но изменит свойства клетки, ее поведение и внутреннюю среду — а значит, и «требования», предъявляемые отбором к другим белкам. Их ландшафты приспособленности станут немного другими. Изменение одного вида в сообществе неизбежно повлияет на факторы отбора, действующего на другие виды, и т. д.
Кроме того, трудно представить себе такой ландшафт, который точно отразил бы реальное соотношение вредных, полезных и нейтральных мутаций. Как правило, большинство мутаций нейтральны — по крайней мере у высших организмов, эукариот, у которых в геномах много участков, слабо влияющих на приспособленность. На втором месте по численности вредные мутации, на последнем — полезные. Нелегко вообразить склон такой формы, чтобы из каждой точки было больше разных путей, параллельных горизонту, чем путей, ведущих вверх или вниз. Но реальные склоны реальных ландшафтов приспособленности именно таковы.
Нейтральные мутации — это по определению такие мутации, которые не влияют на приспособленность, или, что то же самое, не подвергаются действию отбора. Нам пора познакомиться поближе с этим самым распространенным в природе классом мутаций. Забудем на время о ландшафте приспособленности и обратимся к другой модели, которая описывает процессы, происходящие с генетическими вариантами (аллелями) в популяции.
Допустим, у нас есть маленькая популяция мюмзиков из 40 особей. Для простоты примем, что мюмзики гаплоидны, т. е. имеют одинарный набор хромосом — один-единственнный экземпляр генома, а не два, как у нас с вами, диплоидных организмов. Достигнув возраста в один год, каждый мюмзик рожает нескольких детенышей, а потом сразу умирает от старости. Все детеныши одинаковые, но выжить из них могут только 40 — больше мюмзиков просто не помещается в старой железной бочке на дне пруда, где живет изучаемая популяция. Смертность детенышей случайна — ровно 40 случайно выбранных везунчиков станут взрослыми и через год произведут потомство.
Поскольку смертность случайна, приспособленность мюмзиков определяется только их плодовитостью, т. е. числом детенышей. Плодовитость зависит от генотипа. Допустим, у мюмзика есть один ген, влияющий на плодовитость. Обозначим его буквой А. Между прочим, не смейтесь: такая модель вполне годится для изучения некоторых законов популяционной генетики.
Некогда у всех мюмзиков был только один вариант (аллель) гена А. Обозначим его А1. Но потом у одной особи произошла мутация, и в результате появился второй вариант гена — аллель А2. Допустим (опять-таки для простоты), что в нашей популяции, когда мы приступили к ее изучению, у половины мюмзиков ген А был представлен первым вариантом, у другой половины — вторым. Таким образом, частота аллеля А2 равна 0,5 (q2 = 0,5) и частота аллеля А1 такая же (q1 = 0,5).
Нам нужно ответить на вопрос: как будет меняться со временем частота аллеля A2, если мутация, которая привела к его возникновению, была нейтральной?
Раз мутация была нейтральной, значит, плодовитость обладателей обоих аллелей одинакова. Допустим, они все рожают ровно по десять детенышей. Разумеется, потомство наследует родительский аллель гена А.
Может показаться, что раз аллели имеют одинаковую приспособленность, то их так и останется поровну. Это неверный ответ. На рисунке [см. ниже] показан результат четырех запусков нашей модели. Мы видим, что частота А2 во всех четырех случаях хаотически колебалась (по-научному такие колебания как раз и называются случайными блужданиями). Блуждания продолжаются до тех пор, пока частота аллеля не упрется либо в верхнюю «точку невозврата» (q2 = 1, частота аллеля достигла 100 %, аллель зафиксировался в генофонде), либо в нижнюю (q2 = 0, частота упала до нуля, аллель элиминировался из генофонда).
Так бывает всегда. Если аллель нейтрален, его частота будет «случайно блуждать» между нулем и единицей до тех пор, пока не упрется либо в верхний, либо в нижний предел. Рано или поздно нейтральный аллель либо зафиксируется (достигнет частоты 1), либо элиминируется — исчезнет из генофонда. Третьего не дано. Таким образом, блуждания хоть и случайны, их исход предсказуем. Мы точно знаем, что дело кончится либо фиксацией, либо элиминацией. Чем больше популяция, тем в среднем дольше придется ждать исхода[17], но он все равно неизбежен.
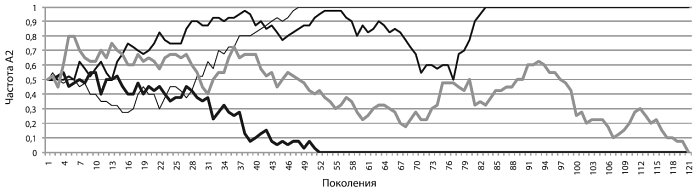
Здесь самое время сказать, что случайные, не зависящие от приспособленности изменения частот аллелей называются генетическим дрейфом. Под властью дрейфа находятся все нейтральные мутации (а в маленьких популяциях отчасти также и вредные с полезными, но об этом позже).
Можно ли вычислить вероятность того, что нейтральный аллель в конце концов зафиксируется, а не элиминируется? Да, это просто. В нашем примере аллели А1 и А2 исходно находились в равном положении, потому что у обоих была частота 0,5. Очевидно, что в такой ситуации шансы на фиксацию у них должны быть одинаковыми и равными 0,5. В половине случаев А1 зафиксируется, А2 элиминируется, в половине — наоборот.
Ну а если конкурирующих нейтральных аллелей не два, а, скажем, четыре и начальные частоты у них тоже одинаковые (0,25)? В этом случае дело кончится фиксацией одного из аллелей и элиминацией трех остальных, причем для каждого аллеля вероятность фиксации равна 0,25. Таким образом, очевидно, что вероятность фиксации нейтральной мутации в будущем просто-напросто равна ее частоте в данный момент: Pfix = q.
Если вы, дорогие читатели, еще не устали от этой примитивной математики, то позвольте познакомить вас еще с двумя простыми, интересными и полезными формулами.
Сколько нейтральных мутаций будет фиксироваться в популяции в каждом поколении? (Имеются в виду мутации уже не в одном и том же, а в разных генах.) Если мы сумеем это вычислить, то получим прекраснейший инструмент — молекулярные часы. Тогда мы сможем по количеству нейтральных генетических различий определить, когда жил последний общий предок сравниваемых организмов.
Вывод этой формулы — подлинный шедевр «биологической математики». Судите сами. Определим сначала, сколько новых мутаций появляется в популяции в каждом поколении. Будем считать для простоты, что подавляющее большинство мутаций нейтральны (это недалеко от истины). Ответ очевиден: U ? N, где U — темп мутагенеза (среднее число новых мутаций у каждой новорожденной особи), N — численность популяции. Определить U можно, просто сравнивая геномы детей и родителей.
Теперь нужно понять, какая часть из этих U ? N только что появившихся мутаций в итоге зафиксируется. Это и будет искомая величина — темп фиксации нейтральных мутаций в генофонде популяции за одно поколение. Обозначим ее буквой V.
Мы уже знаем, что вероятность фиксации мутации равна ее частоте: Pfix = q. Чему же равна частота только что появившейся мутации? Это совсем просто. Поскольку мутация только что появилась, она пока есть только у одной особи. Следовательно, ее частота равна 1/N. Вот, собственно, и все. Умножаем количество новых мутаций на вероятность фиксации каждой из них (т. е. на долю мутаций, которые в итоге зафиксируются) и получаем ответ: V = U ? N ? 1/N. Поразительно! Численность популяции волшебным образом сокращается, и величина N уходит из уравнения. Мы приходим к выводу, что темп фиксации нейтральных мутаций не зависит от численности и равен просто-напросто скорости мутагенеза: V = U. Не знаю, как вы, дорогие читатели, а мы, биологи, приходим в восторг от такой красоты.
Нам остался один шаг до молекулярных часов. После того как два вида, произошедшие от общего предка, разделились, в их генофондах независимо накапливаются нейтральные мутации. За время t (измеряемое в поколениях) первый вид накопит V ? t = U ? t нейтральных мутаций, и второй вид накопит столько же. Совместными усилиями они накопят 2U ? t нейтральных отличий друг от друга. Зная темп мутагенеза U и подсчитав число различий между геномами сравниваемых видов (обозначим его буквой D), определяем время жизни их последнего общего предка: t = D/2U. Это и есть знаменитые молекулярные часы.
Если бы темп мутагенеза и скорость смены поколений были одинаковыми у всех живых существ, все было бы совсем просто. Но они, конечно, неодинаковы, поэтому в вычисления приходится вносить поправки. А еще есть проблема насыщения: в какой-то момент — обычно по прошествии десятков, а чаще сотен миллионов лет — гены разделившихся когда-то видов оказываются настолько «переполнены» нейтральными различиями, что величина D перестает расти, хотя нейтральные мутации продолжают фиксироваться. Ниже мы увидим пример исследования, показавшего, как уровень сходства между «случайно блуждающими» последовательностями приблизился к минимально возможному и дальше снижаться уже не мог.
К счастью, разные участки генома накапливают нейтральные изменения с очень разной скоростью[18]. Быстро меняющиеся участки ДНК используются для датировки недавних событий, а те, что меняются медленно, хороши для датировки событий глубокой древности.
Более 800 000 книг и аудиокниг! 📚
Получи 2 месяца Литрес Подписки в подарок и наслаждайся неограниченным чтением
ПОЛУЧИТЬ ПОДАРОКДанный текст является ознакомительным фрагментом.
Читайте также
«Движение сопротивления»
«Движение сопротивления» Достижения генетиков радуют далеко не всех. В мире уже появились профессиональные борцы с «индустриальной пищей». Они уничтожают посевы с генетически измененными культурами, отказываются от консервов из трансгенных томатов и других
Глава 10 Следы, оставленные три с половиной миллиона лет назад! Дарт, Брум и современные исследователи. Дрейф континентов. Поименный список гоминидов. Люси и ее сородичи.
Глава 10 Следы, оставленные три с половиной миллиона лет назад! Дарт, Брум и современные исследователи. Дрейф континентов. Поименный список гоминидов. Люси и ее сородичи. Столь длительная сохранность доисторических следов у Лаетоли – случай фантастический, но не
ГЛАВА 3 Эволюция земной коры. Дрейф континентов и спрединг океанического дна. Мантийная конвекция
ГЛАВА 3 Эволюция земной коры. Дрейф континентов и спрединг океанического дна. Мантийная конвекция Горные породы, формирующие кору Земли, как мы помним, бывают изверженные — первичные, образовавшиеся при охлаждении и затвердевании магмы, и осадочные — вторичные,
Движение — простейшая форма поведения
Движение — простейшая форма поведения Тропизмы Первое наиболее четкое различие между животными и растениями ясно каждому: растения не могут передвигаться, тогда как животные этим свойством обладают. И тем не менее именно движение растений (поворот к солнцу цветов)
Дрейф и отбор: кто кого?
Дрейф и отбор: кто кого? Генетический дрейф царствует над нейтральными мутациями (аллелями), отбор — над полезными и вредными. Отбор, повышающий частоту полезных мутаций, называют положительным. Отбор, отбраковывающий вредные мутации, — отрицательным, или
ДРЕЙФ ГЕНОВ
ДРЕЙФ ГЕНОВ Иногда эта концепция называется «эффект Сьюэлла — Райта», в честь предложивших ее двух популяционных генетиков. После того как Мендель доказал, что гены являются единицами наследственности, а Харди и Вайнберг продемонстрировали механизм их поведения,
ДРЕЙФ МАТЕРИКОВ
ДРЕЙФ МАТЕРИКОВ В 1912 году немецкий ученый Альфред Вегенер предположил, что около 200 миллионов лет назад все материки Земли составляли единый массив суши, который он назвал Пангеей. В последующие 200 миллионов лет Пангея разделилась на несколько материков, которые стали
Глава 6. Движение
Глава 6. Движение Природы зуб и коготь ал” — это, должно быть, одна из самых цитируемых, к месту и не к месту, аллюзий на Дарвина в англоязычной литературе. Но как бы не к месту ее иногда ни цитировали, эта фраза верно передает если не истинную суть естественного отбора, то,
9.3. Амебоидное движение
9.3. Амебоидное движение Амебы движутся с помощью объемного тока своей цитоплазмы в вырастающие выступы — псевдоподии. В норме они перемещаются по поверхности твердых объектов посредством непрерывного растягивания своих передних концов. Но если до псевдоподий
Движение живых объектов
Движение живых объектов Глядя на то, как двигается тот или иной объект, уже можно сказать, живое ли это существо или просто лист, летящий по ветру. А можно сказать и намного больше. Можно, например, увидеть, что это человек, и увидеть, что он делает. Информации для этого
Движение
Движение О том, что гормоны участвуют в обеспечении движения, известно со времен введения понятия «гормон». Удаление половых желез у самцов приводит к постепенному, но постоянному снижению двигательной активности. В дальнейшем было обнаружено, что она также падает после
3. Ощущение и движение
3. Ощущение и движение Жара повсюду. Ее нельзя больше не замечать. Воздух раскален, как в доменной печи, — он настолько горячий, что мои глаза, защищенные очками, кажутся прохладными по сравнению с остальным лицом. Руки тоже прохладные, но на тыльной стороне перчаток
Движение
Движение «Объединители» и «дробители» этого мира пытаются проникнуть в суть явлений разными путями. Приверженцы классического подхода — объединители — хотят найти то, что объединяет вещи. Они ищут законы, управляющие функциями целого. Мыслители романтического склада
Движение — это сон
Движение — это сон Чего только не делают люди во сне — разговаривают, улыбаются, смеются, плачут, стонут, чмокают, морщатся, вздрагивают, жестикулируют, скрежещут зубами и даже бродят по дому.Людей, которые бы не двигались во сне, не существует. Клейтман исследовал одного
Внутреннее ухо — движение желе и колебание волосков
Внутреннее ухо — движение желе и колебание волосков Представьте себе, что мы заходим в слуховой проход, проходим сквозь барабанную перепонку, мимо трех косточек среднего уха и оказываемся глубоко внутри черепа. Здесь расположено внутреннее ухо — заполненные