3.1.3. ОПРЕДЕЛЕНИЕ ЕВКЛИДА

Отрезок называется разделенным в среднегармоническом отношении, если его большая часть относится к меньшей так же, как весь отрезок относится к своей большей части (рис. 122). Это приводит к появлению пропорции: 1:Х = Х:(1-Х).

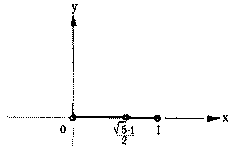
^{Рис. 122. Отрезок называется разделенным в среднегармоническом отношении, если его большая часть относится к меньшей так же, как весь отрезок относится к своей большей части}

Положительный корень соответствующего квадратного уравнения соответствует координате искомой точки. Обычно пользуются его приближенным значением 0,618 для определения длины большей части отрезка, тогда на долю меньшей части приходится 0,382.

Рассеченный в этом отношении отрезок отличается названным выше свойством — особенной соразмерностью своих трех частей — меньшей, большей и целого, воспринимаемых глазом как внутренне уравновешенных. Вслушаемся в название этого принципа по Евклиду: деление отрезка в среднегармоническом отношении. Тема гармонии уже тогда, за 3 века до нашей эры, с очевидностью была обнаружена, правда, пока еще в одномерном пространстве — на прямой.

Оказалось, что и при выходе в пространство большей размерности принцип, указанный Евклидом, по-прежнему создает гармоничное целое, если трехчастность его формы подчиняется действию евклидовой пропорции.

Мы уже упомянули пример хорошо сложенного человека, у которого горизонтальная линия, проведенная через пупок, отвечает среднегармоническому сечению. Это давало скульпторам и художникам один из гармонических канонов для определения правильных продольных пропорций человеческого тела. Впоследствии выяснилось, что идеальное строение человека и в целом, и в деталях подчиняется евклидову числу и соответствует классическим представлениям о красоте (Фидий, и в честь его Φ = ¹/_X, где X — число Евклида).

^{Рис. 123. Форма головы воспринимается художником совершенной, если отношение ее поперечного и продольного диаметров в точности соответствует Евклидову числу}

Приведем отдельные примеры.

Форма головы воспринимается художником совершенной, если отношение ее поперечного и продольного диаметров в точности соответствует евклидову числу (вспомним овал лица, который есть не что иное, как продольное сечение яйца, рис. 123).

Канон женской красоты (рис. 124) определяется отношением талии к бюсту, равным отношению талии к бедрам и равным числу Евклида.

^{Рис. 124. Канон женской красоты определяется отношением талии к бюсту, равным отношению талии к бедрам и равным числу Евклида}

Канон мужской красоты (рис. 125) определяется этим же числом по-другому: здесь евклидовой пропорции соответствует отношение ширины в бедрах к ширине в плечах.

^{Рис. 125. Канон мужской красоты определяется по-другому: здесь Евклидовой пропорции соответствует отношение ширины в бедрах к ширине в плечах}

Внимательный читатель сразу усмотрит в этом проявление полового диморфизма и найдет соответствующее функциональное объяснение.

Оказывается, что под действие евклидова сечения подпадает не только гармония человека: всемирно известные архитектурные строения своими пропорциями также повторяют это число (пирамиды Хеопса, Хефрена и Микерина, Парфенон, театр Диониса в Афинах, церковь Покрова на Нерли, храм Василия Блаженного, церковь Вознесения в Коломенском, система «Модулор» Ле Корбюзье…), ему соответствуют примеры из самых неожиданных областей, о которых мы расскажем позже.

И во всех воплощениях, живых и неживых, форма, рождаемая принципом Евклида, вызывает ощущение гармонии, содержащей в себе внутреннее движение, гармонии напряженной, являющейся антиподом гармонии покоя. Таким образом, наряду с буквальной законченностью симметричной формы и ее статичным равновесием возникает парадоксальная завершенность внутренне напряженной формы, сбалансированность частей которой определяется принципом среднегармонического сечения.