Глава A. Аналоговые таблицы генетического кода (XIII)

We use cookies. Read the Privacy and Cookie Policy

Глава A.

Аналоговые таблицы генетического кода (XIII)

Первым, кто попытался упорядочить таблицу генетического кода и построить ее на рациональной основе, был наш выдающийся ученый Юрий Борисович Румер. Он был физиком, учеником Макса Борна, хорошо знал Альберта Эйнштейна, Пауля Эренфеста, Эрвина Шредингера, был другом Льва Ландау. Читал лекции в Московском университете, работал в ФИАНе. Само собой, очередная российская власть (большую часть ХХ века – советская) привычно обошлась с крупным ученым, сунув его в 1938г в лагерь, а потом в авиационную шарашку, где он работал с Туполевым, Королевым, Мясищевым, Петляковым, Глушко, Бартини, Карлом Сциллардом, братом упоминавшегося выше Лео; каждый незауряден. Ольга и Сергей Бузиновские55 показывают целую вереницу выдающихся людей, которая незримо тянется за именем Румера – от Понтекорво до Ферми и Александра Грина, от Флерова до Сент-Экзюпери и Алексея Толстого, от Бартини до Ильфа и Петрова и Булгакова…

…В 1953г Румер был реабилитирован, потом работал в Академгородке под Новосибирском. Как только Ниренберг с соавторами опубликовали в 1965г полный словарь генетического кода, Румер немедленно погрузился в эту тематику. В том же году он писал: «Рассмотрение группы кодонов, относящихся к одной и той же аминокислоте, показывает, что в каждом кодоне (XYZ) целесообразно отделить двухбуквенный корень /XY/ от окончания /Z/. Тогда каждой аминокислоте, в общем случае, будет соответствовать один определенный корень, а вырожденность кода является следствием изменения окончания». Шестнадцать возможных корней он разбил на два октета (с заменой тимина Т на урацил U для РНК):

Идея о разбиении корней кодонов на два октета – «сильные» и «слабые» была совершенно новой и неожиданной для специалистов, работавших в этой области. Оказалось, что анализ многих свойств аминокислот четко подтверждает разбиение всех аминокислот на две группы, соответствующие разбиению корней на два октета. Исследованию разнообразных следствий этой идеи были посвящены несколько работ Румера. В частности, подход Румера к проблеме с однозначностью приводил к следующему порядку букв:

C – очень сильная

G – сильная

U – слабая

A – очень слабая

Этот порядок букв (CGUA) дает возможность сформулировать простые правила, определяющие «силу» корня:

сила корня, содержащего в качестве второй буквы С или А, определяется

силой второй буквы;

сила корня, содержащего в качестве второй буквы G или U, определяется силой первой буквы.

Крик предпочитал другой порядок букв в генетическом алфавите. В письме Румеру он доказывал преимущества порядка UCAG (этот порядок и сейчас используется во всех учебниках), но алфавит Румера позволял, в частности, видеть поразительные симметрии внутри генетического кода. Не вдаваясь в описание румеровской аргументации, мы предлагаем здесь свой порядок: CUAG, основанный не на качественном понятии «сила кодирующего основания», но на простом упорядочивании по нарастанию весьма простого же параметра – молекулярной массы азотистых оснований – и показываем группу наглядных симметрий, что – как и сам принцип такого упорядочивания – представляется нам даже более интересным. Но об этом позже. Что же до Юрия Борисовича Румера, то это фигура чрезвычайно интересная; о н?м очень много можно прочесть в Интеренете:

…Чуть? у Румера было поразительным. То, что увлекало его в молекулярной биологии [много] лет назад, сейчас является передним краем исследований. В последние годы наблюдается явный рост числа публикаций, в которых проблемы генетического кода анализируются с привлечением симметрий и методов теории групп. Предлагаются разные подходы, основанные на разных типах групп, включая квантовые. В основном этим занимаются физики, не слышавшие о работах Юрия Борисовича. Когда они знакомятся-таки с работами Румера, то поражаются их изяществу, глубине и тому, что идеи симметрии уже [много] лет назад играли центральную роль при подходе к проблемам генетического кода…

Любопытно, в частности, что Юрий Борисович инициировал исследования и по поиску корреляций между одномерной и трехмерной структурами белков. Их не удалось довести до конца по причине существенной неполноты экспериментальных данных, отсутствия хороших компьютеров, а в основном, по-видимому, из-за недостатка энтузиазма… у молодых участников проекта. И снова современное: Не люблю я точные науки, Точно сам не знаю, почему…

Он объединил кодоны, третья буква которых может быть любой из четырех, в один набор, а кодоны, не удовлетворяющие этому условию – в другой. Оба набора содержали равное число триплетов – по 32 каждый. При этом число кодирующих дублетов в обоих наборах составляло по восемь в каждом, поэтому наборы были названы октетами. Оба октета оказались связанными между собой простым преобразованием: T?G, C?A (ДНК-вариант):

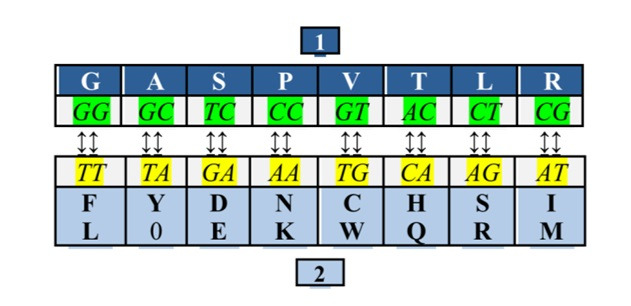
Этот рисунок иллюстрирует румеровское преобразование, переводящее дублеты одного октета в другой. Третье основание кодона неявно присутствует здесь в составе октета II, продукты которого организованы в две строки: верхнюю кодируют триплеты с третьим пиримидином, нижнюю – с третьим пурином.

Идеи Юрия Румера были продолжены и развиты работами Владимира Щербака. Два румеровских октета Щербак преобразовал таким образом, чтобы выделить в них группы вырожденности, пронумеровав их справа налево, а продукты кодирования (аминокислоты) он упорядочил в каждой группе по нарастанию молекулярной массы слева направо; триплеты, соответствующие продуктам кодирования, он записал по вертикали сверху вниз. Тогда первые, вторые и третьи основания кодонов образовывали три строки в каждом кодоне. Вот что у него получилось (цифры под третьими основаниями – характеристики кодируемого продукта):

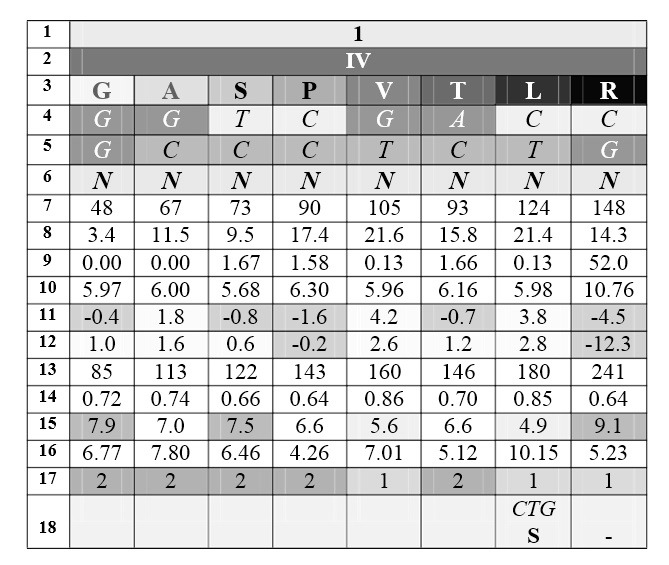
1. номер октета

2. номер группы вырожденности

3. продукт кодирования (аминокислота или терминирующий сигнал 0)

4. 1-е основание кодона

5. 2-е основание кодона

6. 3-е основание кодона

7. Bulkiness (мера формы или объ?ма или «громоздкости» боковой цепи)

8. Объем (рассчитанный по Ван-дер-Ваальсовым радиусам)

9. Полярность (сила электрического поля вокруг молекулы)

10. Изоэлектрическая точка

11. Гидрофобность 1; гидрофильные аминокислоты – выделены темносерым и отрицательными значениями

12. Гидрофобность 2 (другие данные)

13. Поверхность, доступная для воды в развернутом пептиде

14. Доступная воде поверхность, теряемая при свертывании пептида

15. Polar requirement, PR (эмпирические данные по хроматографии водных растворов). Темный> 7.5; светлый <5.6

16. Частота встречаемости аминокислот в белках современных организмов

17. ars-класс

18. неканоническое кодирование ( – нет продукта)

В двух прямоугольных блоках – два румеровских октета (строка 1), упорядоченные по нарастанию номера, каждый из которых разделен на группы вырожденности, помеченные соответствующими римскими цифрами (строка 2) и упорядоченные по убыванию номера. Строка 3 – продукты кодирования, упорядоченные по нарастанию масс в «своих» группах вырожденности (что – как и в первых двух случаях – подчеркивается градиентом насыщенности серого цвета). Символы оснований кодирующих триплетов расположены вертикально – сверху вниз, от 5` до 3` – для удобства сравнения кодонов по первым, вторым и третьим буквам соответственно. Четное содержание продуктов кодирования в октетах позволяет провести посередине вертикаль, которая оказывается осью симметрии по отмеченным ниже характеристикам. R – пурины (A, G), Y – пиримидины (С, Т), N – любое из четырех азотистых оснований. 0 – стоп-кодон. Строки 7—15 – физико-химические свойства аминокислот.

Эта несложная организация приводит к поразительно красивой общей картине: в октете 1 первые основания триплетов (первая строка) оказываются взаимно комплементарными относительно упомянутой вертикали; вторые основания – зеркально симметричны по пуринам и пиримидинам. Симметрия третьих оснований – это симметрия их монотонного ряда. Симметрии подчеркиваются оттенками серого (интенсивность которого нарастает с увеличением молекулярной массы продукта кодирования в составе группы вырожденности).

Симметрия кодирующих триплетов и продуктов кодирования, относящихся к октету 2, в этой таблице немного сложнее, но также вполне наглядна. Она требует двух предварительных пояснений. Первое – это позиция цистеина, С. Универсальный код предписывает дублету TG кодирование цистеина, если третьим основанием кодона является пиримидин Y, а кодирование триптофана, если третья буква кодона – G. Аденин в третьей позиции образует пунктуационный знак – стоп-кодон TGA. То обстоятельство, что при этом нарушается симметрия, ставит определенную проблему, которую Владимир Щербак разрешил, обнаружив, что обозначенная в таблице позиция цистеина принципиально не противоречит Природе, поскольку существуют одноклеточные микроорганизмы (Euplotida, реснитчатые, инфузории), генетический код которых отличается от универсального как раз по кодированию цистеина: триплет TGA у них транслируется как С и не имеет функции «стоп». Второе пояснение относится именно к функции «стоп», которая рассматривается в таблице как «законный» продукт кодирования, не имеющий массы.

Итак, упорядочивание продуктов кодирования октета 2 по нарастанию молекулярной массы так же, как и в случае октета 1, приводит к симметриям первых, вторых и третьих оснований соответствующих кодонов. При этом основной особенностью этого представления является зеркальная симметрия пар кодирующих дублетов пяти краевых позиций и симметрия со сдвигом трех пар внутренних, кодирующих триплетов. Так же, как и в октете 1, осью этой симметрии является вертикаль, которая делит строки точно посередине. Симметрию третьих оснований нечетных групп вырожденности (H|G) Владимир Щербак рассматривал в данном случае как вариант симметрии Y|R.

Как мы упоминали, симметрия описанного представления генетического кода имеет место не только по молекулярной массе аминокислот, но и по другим их параметрам (строки 11—15). Замена в третьей позиции пары симметричных кодонов пурина пиримидином – и наоборот – в определенной мере сохраняет, например, гидрофобность кодируемых продуктов, хотя размер аминокислоты при этом, конечно, основательно меняется. Однако, ни гидрофобность, ни еще одна характеристика – PR (строка 15) – которую Карл В?зе и его группа описали, как основу регулярности генетического кода и соответствия кодонов и продуктов кодирования, не могут сравниться по строгости симметрий с молекулярной массой аминокислот, что хорошо демонстрирует приведенная таблица Владимира Щербака. Неканонические ключи кодирования (строка 17) тоже выглядят в этих таблицах довольно беспорядочными и случайными отклонениями.

За весь этот рисунок кооперативной симметрии генетического кода, на основе молекулярных масс его компонентов, за ее красоту и гармонию, не имеющую к тому же сколько-нибудь внятного физического, химического или молекулярно-биологического обоснования, мой друг назвал описанную таблицу каллиграммой (красивой записью). Термин этот принадлежит Гийому Апполинеру, который – в экспериментальном порядке попытался организовать некоторые свои тексты так, чтобы продемонстрировать их симметрию. Их он и называл calligrammes.

В следующей главе мы покажем, что симметрии каллиграммы Щербака имеют неожиданный количественный характер, то есть, по-видимому, даже более сущностны, нежели только что описано. Стоит, однако, отметить, что известные небольшие отклонения от универсального генетического кода могут серьезно нарушать симметрии каллиграммы. Например, генетический код митохондрий позвоночных, который, по одним представлениям, был предшественником универсального, а по другим – сам происходил из него, отличается тем, что у него отсутствуют нечетные группы вырожденности, так что две четные прямо соответствуют двум октетам Румера. При этом дублет TG кодирует цистеин, если в третьей позиции триплета стоит пиримидин, и триптофан, если в третьей позиции – пурин. То же относится и к дублету АТ: ATY=I, ATR=M. И еще одно отличие от универсального: триплет AGR кодирует не аргинин, а сигналы терминации (0). Это означает, что описанная каллиграмма Щербака, сама по себе, как будто, не является обязательным условием организации генетического кодирования (земных?) организмов. Вместе с тем, Андрей Хренников и Сергей Козырев56, используя так называемые р-адические числа, показали наличие значительной регулярности и в этой версии генетического кода. Автор не берется комментировать их работу, поскольку ровно ничего не понимает в р-адических числах и в d-адических плоскостях. Однако, она каким-то образом связывает регулярную организацию (в том числе и симметрии) генетического кода с его защищенностью. В своих рассуждениях Хренников и Козырев отталкивались от представления кодирующих триплетов, предложенного Роз-Мари Свансон5757 и позднее уточненного Драганом Босняцким5858 с соавторами на основе подхода, используемого для решения хорошо известной Проблемы Путешествующего Продавца (ППП). В этом представлении последовательность кодирующих триплетов образует цикл, известный как «код Грея»:

Напомню, что кодом Грея называется любая циклическая последовательность всех наборов из нулей и единиц, в которой два соседних набора отличаются только по одной компоненте (дельта Хемминга). Другими словами, код Грея – это система замкнутой организации числового ряда, в которой два соседних значения различаются только в одном разряде. Вот как выглядит 3-битный двоичный код Грея (каждое трехзначное число представлено здесь вертикально; то есть чтение его сверху вниз соответствует обычному чтению слева направо) в линейном представлении:

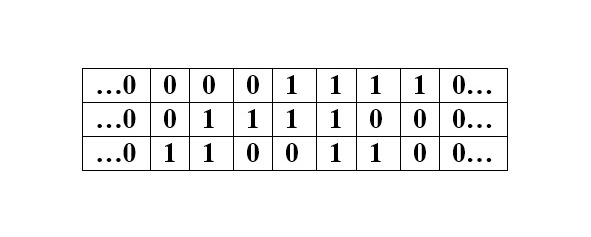
Первое и последнее числа (000) совпадают, указывая на замкнутость ряда. Читателю предлагается обратить внимание на то, что числа кода Грея (двоичные в данном случае) расположены в последовательности, не совпадающей с натуральным рядом: преобразованные в десятичные, они дают здесь последовательность 0—1—3—2—6—7—5—4—0.

В представлениях Свансон и Босняцкого кодировка Грея образует последовательность наборов (3-компонентных наборов, то есть, триплетов из 4-х оснований), в которой два соседних набора отличаются только по одному основанию (в одной и той же позиции). В последовательности, организованной по этому правилу, различаются (хотя и не слишком строго) группы, соответствующие размерам аминокислот («большим» и «малым»), а также их позициям в составе белковых молекул («наружным» или «внутренним», то есть, гидрофильным или гидрофобным). Описанное свойство дает генетическому коду дополнительную защищенность. Стоит вспомнить, что – как об этом пишет Википедия – «коды Грея широко используются для упрощения выявления и исправления ошибок в системах связи, а также в формировании сигналов обратной связи в системах управления». Они применяются и в теории генетических алгоритмов для кодирования генетических признаков, представленных целыми числами, поскольку минимизируют эффект ошибок при преобразовании аналоговых сигналов в цифровые.

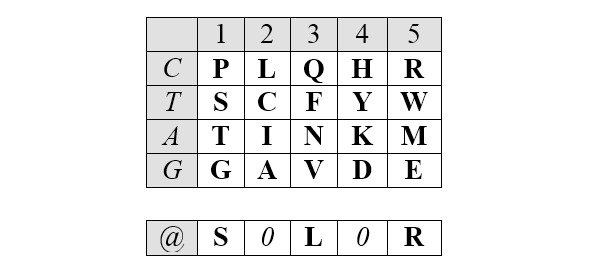
Часть аминокислот обладает выраженными гидрофильными или гидрофобными свойствами. Молекулы синтезируемого полипептида сворачиваются в фиксированную трехмерную структуру. Основной параметр, определяющий это сворачивание (фолдинг) – гидрофобность или гидрофильность аминокислоты. Код очевидно не мог эволюционировать по размеру кодона; он с самого начала был триплетным, что определялось физикой комплементарных соответствий. Что до функций каждой буквы триплета, то поскольку в современном коде за гидрофобность аминокислоты отвечает центральный нуклеотид, постольку на начальных этапах эволюции кодирования направление считывания кодона, по-видимому, не имело большого значения. А общий паттерн генетического кода потребовал симметрий как условия помехоустойчивости хранения, передачи и приема информации, и соответствующие функции были делегированы краевым основаниям триплета. После установления вектора считывания кодона эти функции были, по преимуществу, отданы первым буквам, в то время, как половина третьих стала просто межкодонными разделителями, а вторая половина – дискриминаторами для продуктов с общим кодирующим дублетом. И в этом случае (то есть в случае вторых кодонных оснований) порядок CTAG выявляет билатеральную симметрию:

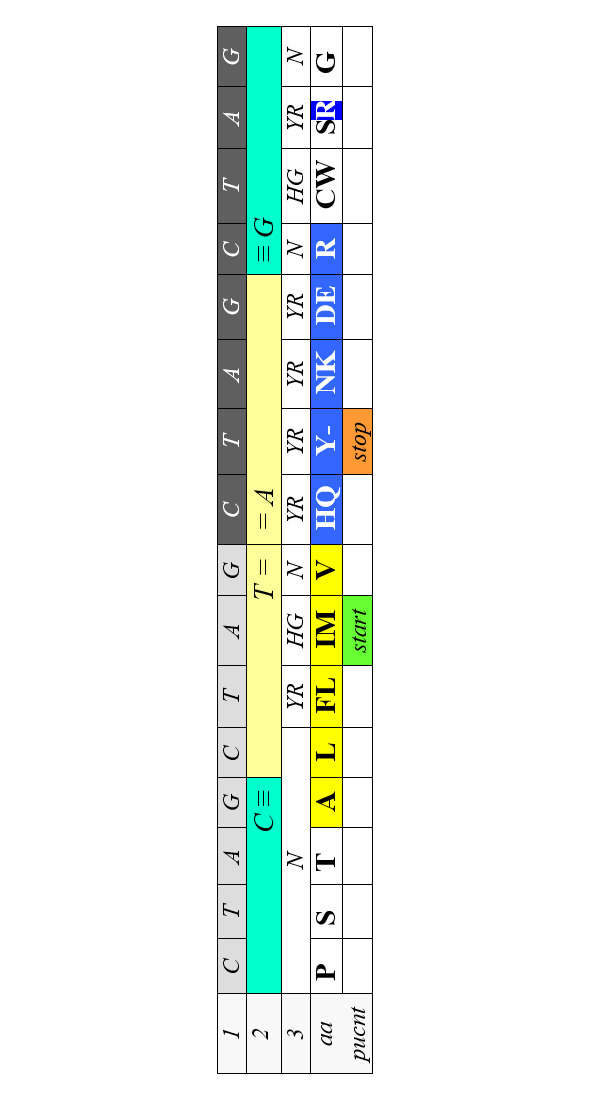
То обстоятельство, что позиции гидрофильных и гидрофобных аминокислот выходят за пределы «своей» центральной буквы в обе стороны от оси симметрии (между Т и А в этой таблице, еще раз подчеркивает значение порядка CTAG в организации генетического кода. Так же симметрично в Таблице 4 размещаются и некоторые другие продукты кодирования – например, пунктуационные знаки.

Вернемся, однако, к молекулярной массе как таковой. Автор использовал этот параметр не только для характеристики кодируемых продуктов, но также для характеристики кодирующих оснований. Упорядочивание азотистых оснований по нарастанию массы приводит к ряду C <T <A <G (или C <U <A <G, что в данном случае дела не меняет). Основания ряда симметричны относительно середины, которая делит его на две пары зеркально расположенных оснований CG и ТА (о чем мы уже говорили). Этот ряд не совпадает с рядами Крика и Румера, положенными в основу соответствующих таблиц кода, но Автор находит его намного более интересным и рациональным. Он мгновенно преобразует хорошо известную стандартную таблицу универсального генетического кода (Глава G@C), кочующую из учебника в учебник, в симметричную по группам вырожденности относительно оси, разделяющей первые кодирующие пиримидины и пурины (см. следующую страницу).

В новой таблице хорошо разделяются кодоны октетов 1 и 2; последние образуют светлую фигуру «креста», в которой, в свою очередь, хорошо заметно симметричное – относительно центра фигуры – расположение нечетных групп вырожденности и триплетов, дополняющих в октете 2 кодирование аминокислот S, L и R, имеющих свои кодоны в октете 1.

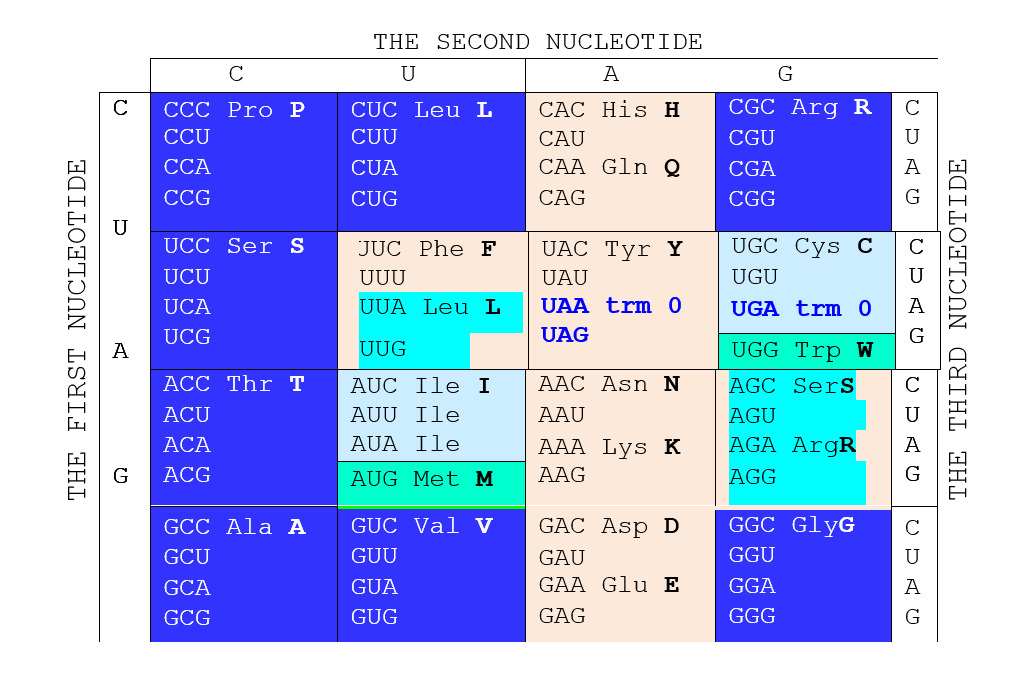
Упорядочивание кодируемых аминокислот по массе неожиданно выявляет еще одну группу симметрий, которые связаны с классом аминоацил-тРНК-синтетаз (АРСаз), присоединяющих аминокислоту к тРНК. АРСазы делятся на два класса на основе структурного сходства и способу аминоацилирования тРНК. АРСазы 1-го класса (АРСазы-1) в большинстве случаев мономеры. 76-й аденозин тРНК они аминоацилируют по 2» -ОН группе. АРСазы-2 – это, как правило, димеры. За исключением фенилаланил-тРНК-синтетазы все они аминоацилируют 76-й аденозин тРНК по 3» -ОН группе. Оба класса АРСаз содержат равное число ферментов – по десять в каждом. Кроме того, АРСазы-1 узнают «свою» тРНК со стороны так называемого «малого желобка» акцепторной миниспирали, а АРСазы-2 – со стороны «большого».

Разделим по аналогии с АРСазами-1 и -2 – соответствующие им аминокислоты также на два класса арс-1 и арс-2. При этом возникает внятная билатеральная симметрия двадцатки аминокислот: ровно половина из них (мы здесь не вдаемся в детали), синтезируется с помощью аминоацил-тРНК-синтетаз (АРСаз) I класса:

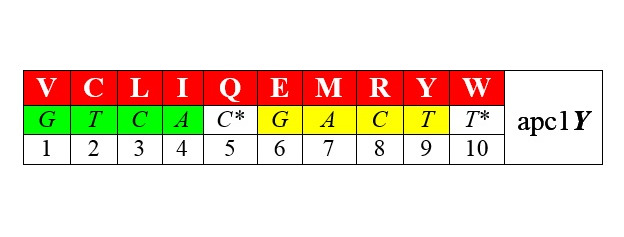
Другая половина синтезируется с помощью АРСаз II класса (нижние строки – порядковые номера аминокислот при раздельной – по классам [1—10 и 1—10] и при сплошной [1—20] их нумерации):

В обоих представленных рядах аминокислоты упорядочены по нарастанию молекулярной массы. Любопытно, что в каждый арс-класс попадает по три неполярные алифатические аминокислоты (VLI и GAP), по три полярные незаряженные (CQM и STN), по одной негативно и позитивно заряженных (E-R+ и D-K+) и по две ароматические (YW и HF) аминокислоты. В каждой из строк первых букв кодирующих эти аминокислоты триплетов легко различаются две четверки GTCA и GATC, разделенные в одном случае пиримидинами С* и Т*, в другом – пуринами G*и А*. Поэтому арс-1 мы условно называем пиримидиновыми аминокислотами арс-Y, а арс-2 – пуриновыми, арс-R. Как это может соотноситься с молекулярной биологией процессов, связанных с трансляцией, мы увидим далее.

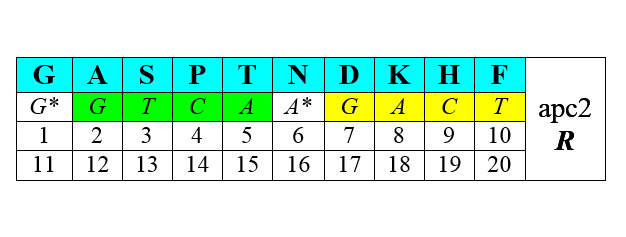
Описанные симметрии рядов арс-Y и арс-R сохраняются и в двумерном (2D) представлении. Это представление, образно (то есть, не математически) названное Автором базовой матрицей генетического кода, формируется абсциссой, вдоль которой размещаются аминокислоты, упорядоченные по нарастанию молекулярных масс, и ординатой, вдоль которой размещаются первые кодирующие основания, соответствующие этим аминокислотам.

Базовая (без нижней дополнительной строки) матрица является прямоугольником 4х5, содержащим двадцатку канонических аминокислот. В отличие от каллигаммы, матрица не требует специального допущения для кодирования цистеина и, таким образом, полностью соответствует универсальному генетическому коду. Центральные колонки матрицы отчетливо структурированы по гидрофильности аминокислот (в таблице ниже – светлые ячейки заняты гидрофобными аминокислотами, темные – гидрофильными):

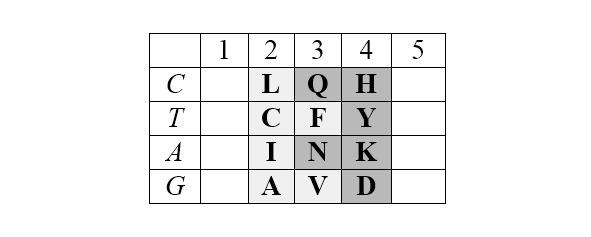
Матрица структурирована также по позициям обозначенных выше четверок аминокислот обоих арс-классов, демонстрируя их строгую сдвиговую симметрию:

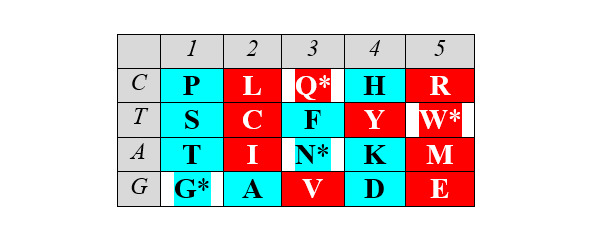
Отчетливо заметна и симметрия продуктов, маркирующих деление арс-классов аминокислот на «пуриновые» и «пиримидиновые», – относительно центральной колонки матрицы:

Поскольку в каждой строке матрицы не более двух или трех аминокислот одного класса с хорошо различимой массой, то при способности АРСаз узнавать хотя бы первое основание кодона (третье – антикодона) и отличать его от фиксированного по массе реперного соседа, безошибочное узнавание АРСазой «своей» тРНК чрезвычайно упрощается. Таким образом, матрица хорошо иллюстрирует решение парадокса множественного узнавания небольшой молекулы с почти монотонной структурой.

Заканчивая главу, упомянем еще об одной нашей находке, имеющей отношение к кодовым симметриям. Оказывается, продукты кодирования зеркально-симметричными дублетами (типа ABN и BAN) следуют трем простым правилам:

при нарастании массы оснований в дублете кодируемый продукт имеет большую молекулярную массу, при снижении – меньшую;

молекулярная масса продукта, кодируемого гомотриплетом (то есть, ССС, ТТТ, ААА, GGG), больше, если триплет составлен из пиримидинов;

молекулярная масса пары аминокислот, кодируемых гомодублетом (то есть, СС-, ТТ-, АА-, GG-), больше, если он состоит из пиримидинов.

Возникает вопрос, какой смысл – и есть ли он – в кодовых симметриях и соотношениях, описанных в этой главе? Если хиральность биологических молекул и клеточная организация имеют очевидные достоинства и являются необходимыми для возникновения жизни и последующей эволюции, то симметрия (в первую очередь, билатеральная) генетического кодирования, по меньшей мере, озадачивает. Является ли она следствием каких-то не открытых еще физических или информационных законов (например, исходных альтернатив, выбор которых имел селективные преимущества, похоронившие первые версии кода, значительно более разнообразные и не столь регулярные)? Имеет ли она отношение к надмолекулярным симметриям биологических форм? Нужна ли подобная симметрия кода для его невероятной стабильности или для максимальной простоты и надежности его функционирования в биологических системах? Положительные ответы на все эти вопросы весьма соблазнительны, но без весьма основательной проработки – остаются лишь гипотезами, доказательства которых сегодня даже не просматриваются. Альтернативная точка зрения (Френсис Крик) заключается в том, что все эти симметрии совершенно случайны, и генетический код мог быть каким угодно: химического соответствия между аминокислотами и антикодонами нет. И если сегодня – в большинстве случаев – нельзя рассчитывать на то, что после замены антикодона на другой в синтезируемый полипептид войдет аминокислота, соответствующая новому антикодону, то это потому только, что длительная эволюция – опять-таки во многих случаях – оптимизировала соответствие АРСаз и тРНК за счет участков, выходящих за пределы антикодона.

Следующая глава написана для тех читателей, кого обе точки зрения оставляют в состоянии умственного дискомфорта. Но только те из них, кто разделяет черный оптимизм Автора, кто понимает, что если не веришь в Бога, то это не означает автоматическую «веру в Большой Взрыв», и кто не ждет от науки неизбежного разрешения ассонанса в консонанс (не органчик же!), – только они получат удовольствие от того, что ответы на эти вопросы вызывают новые, еще более острые.

…………………

Сразу ясно, что символом А эта глава названа просто потому, что речь в ней идет об аналоговых представлениях генетического кода. Здесь мы, наконец, оставляем без внимания множество «интересных» чисел, которыми до сих пор докучали терпеливому Читателю, но к которым вс? же ненадолго вернемся в последующих двух главах, посвященных оцифровке приведенных выше аналоговых представлений.

Данный текст является ознакомительным фрагментом.