Глава третья Энергия Универсализация бухгалтерии
Глава третья
Энергия
Универсализация бухгалтерии
Энергия — это вечный восторг.
Уильям Блейк
Великая идея: энергия сохраняется
Ни пульсация биосферы, возникшая из неорганической Земли, ни молекулярная активность, поддерживающая и расширяющая ее сегодня, не могли бы существовать без притока энергии от Солнца. Но что это за вещь, которую мы называем энергией? Это слово может сорваться с губ каждого, а ученый может увидеть в нем то, что связывает Вселенную в постижимую и живую целостность; но что это такое на самом деле?
Поэты, в своей неподражаемой манере, создали концепцию энергии задолго до того, как она попела в поле зрения ученых. Так сэр Филип Сидни, в своей, написанной в 1581 г., Защите поэзии привлек внимание к «тому, что есть мощь или Energie (как называли ее греки) писателя». Он имел в виду скорее энергичность выражения, чем характеристику движения пули, вылетевшей из мушкета, которая впоследствии убила его. Греки действительно называли это, что переводится буквально как «работа», и мы можем уловить этимологический путь, приведший к понятию литературной энергичности. В наши дни широкая публика приняла такое понимание энергии близко к сердцу и уверила себя, будто точно знает, что это такое, находит это ценным, чувствует существенный вклад этого в современный мир и страшится перспективы утраты этого.
Энергия все еще является объектом литературного дискурса, но она получила новую, богатую и точно очерченную жизнь в науке. Так было не всегда. Научное использование этого термина может быть прослежено вспять до 1807 г., когда Томас Юнг (1773-1829), занимавший должность профессора натурфилософии в такой твердыне науки, какой было Королевское общество Великобритании, а позднее, в замечательно универсальном духе времени, внесший вклад в расшифровку надписи на розеттском камне, конфисковал этот термин для науки, когда написал, что «термин энергия может быть с великим удобством применен для обозначения произведения массы или веса тела на квадрат численного выражения его скорости». Как и многие пионерские сообщения, заявление Юнга о «великом удобстве» оказалось полупропечённым, и нам придется приложить некую работу, чтобы завершить его выпечку. Проделав ее, мы придем к пониманию современной интерпретации энергии и увидим значение и важность ее сохранения.
Чтобы уловить суть природы энергии, нам необходимо понять две очень важные вещи, касающиеся событий и процессов в мире. Одна касается характеристик движения тел в пространстве; другая — природы теплоты. Описание движения в пространстве было в основном завершено к концу семнадцатого столетия. Потребовалось на удивление долгое время, чтобы сразиться с природой тепла и в конце концов одержать победу. Этой цели не удавалось достигнуть до середины девятнадцатого века. Как только движение и тепло были поняты, ученые успешно расправились и с природой событий. Или так они в то время думали.
Греки размышляли о движении тел, хотя и без всякой пользы, и две тысячи лет держали мир в заблуждении: их стиль вопрошания из кресла гораздо лучше подходил для математики и этики, чем для физики. Так, Аристотель (384-322 до н.э.) умозаключил, что стрела удерживается в полете действием воздушных вихрей, создаваемых ею, и поэтому сделал вывод, что в вакууме стрела должна быстро остановиться. Как это часто бывает, наука проясняет вопрос, превращая общепринятое мнение в противоположное, и мы теперь знаем, что верно в точности обратное: сопротивление воздуха замедляет движение стрелы, а не толкает ее вперед. Свидетельств о необходимости поддерживающей силы в те тяжкие времена было множество, ибо рогатому скоту приходилось напрягаться, чтобы удерживать в движении скрипучие деревянные повозки. Абсурдно было бы думать обратное, ведь тогда селянам пришлось бы запрягать рогатый скот позади движущейся телеги, чтобы остановить ее естественное движение. Изобретательный ум Аристотеля увидел в воздухе вихри, толкающие стрелу вперед и тем самым спасающие его теорию.
Аристотель имел и более общие иллюзии относительно причины событий и движения объектов. Как феноменологические рассуждения, его иллюзии были вполне осмысленными, и он заслуживает восхищения за непрестанный поиск объяснений и выпытывание у Природы ответов. Однако, помимо абсолютной ложности, его мнения были лишены того, что мы сегодня называем объяснительной силой, и совершенно не поддавались переложению на язык цифр. Например, он представлял себе ряд концентрических сфер со сферической Землей в центре, окруженной последовательно сферой воды, сферой воздуха и сферой огня, а все это в целом заключено в хрустальные сферы небес. В его модели вещество искало свое природное место, так, первоначально подброшенные кверху земные объекты падали на Землю, а языки пламени рвались наверх, стремясь к своему природному обиталищу. Легко отыскать дыры в этой модели с нашей современной точки зрения, но она владела умами людей на протяжении двух тысячелетий, возможно, потому, что люди находились во власти традиции, требовавшей учиться у авторитетов, не полагаясь на собственные наблюдения, или, может быть, потому, что в упражнениях своей любознательности им недоставало мужества, необходимого для того, чтобы противопоставить наблюдения авторитету.
Главным вкладом Галилея в эту конкретную историю было то, что он сбросил с глаз повязку авторитетных мнений и, с открытыми для наблюдений глазами, продемонстрировал ложность аристотелевой версии событий. Галилей постулировал, что если тело не подвергается действию силы, то оно сохраняет состояние своего движения. Он пришел к этому заключению, наблюдая скатывание шара по наклонной плоскости и последующее вкатывание на противоположную плоскость, и заметив, что, каков бы ни был угол наклона второй плоскости, шар подымается на одну и ту же высоту. Он заключил, что, если бы вторая плоскость была горизонтальной, шар катился бы вечно, поскольку никогда не достиг бы первоначальной высоты. Введение наклонной плоскости было само по себе гениальным приемом, поскольку оно замедлило процесс падения тела до такой степени, что его стало возможно изучать количественно и с большой точностью, и таким образом представление открыло путь наблюдению.
Это заключение Галилея стало поворотным пунктом в науке, поскольку оно подчеркнуло силу абстракции и идеализации, о которых я упомянул в Прологе, причем последняя дала возможность пренебречь побочными факторами, затемняющими суть эксперимента. Конечно, Галилей никогда явно не демонстрировал, что шар будет вечно катиться и катиться, и в любом эксперименте этого рода реальный шар на деле рано или поздно остановится, очевидно и несомненно следуя Аристотелю. Однако Галилей понял, что бывают существенные компоненты поведения с одной стороны и побочные влияния с другой. Последние включают трение и сопротивление воздуха: уменьшая их (например, полируя шар и поверхности плоскостей), он мог приблизиться к идеальной ситуации и выявить суть поведения шара. В мире аристотелевского опыта, где рогатый скот тяжко топает по грязи, таща тяжелые повозки, побочные влияния полностью затопили суть поведения повозки.
Факел Галилея перешел к Ньютону. В соответствии со старым календарем Исаак Ньютон[11] (1642-1727) родился в год смерти Галилея (рис. 3.1), так что романтически настроенные любители признаков реинкарнации могут усмотреть здесь переселение души. В отличие от Галилея, Ньютон по всем описаниям был весьма сварливым и вздорным человеком, но он также был одним из величайших ученых. Почти в одиночку он привел математику на службу физике и таким образом открыл дорогу для современной количественной физической науки. Он сделал больше, он изобрел математику, которая была ему нужна для осуществления его программы, и его Principia[12], опубликованные в 1687 г., являются памятником мощи человеческого интеллекта, приложенного к решению проблемы рационализации наблюдений.

Рис. 3.1. Ньютон и современная физика родились в этой комнате утром в день Рождества 1642 г. Мебель не является подлинной.
Пять аксиом Эвклида для формулирования геометрии, которую мы исследуем в главе 9, полностью задают структуру пространства, и с их помощью мы узнаем, где мы находимся. Три закона Ньютона полностью задают движение в этом пространстве, и с их помощью мы узнаем, куда мы направляемся. В немного упрощенном виде они выглядят так:
1. Тело продолжает равномерное движение по прямой линии, если оно не подвергается действию силы.
2. Ускорение тела пропорционально приложенной силе.
3. Каждому действию всегда противостоит равное противодействие.
Из этих трех простых утверждений вырастает все здание классической механики, как называется описание движения, основанное на законах Ньютона, а также понимание и предсказание движения частиц, снарядов, планет, а в наши дни также спутников и космических кораблей.
Первый закон Ньютона есть простое повторение формулировки анти-аристотелевского наблюдения Галилея, и иногда его называют законом инерции.
Его второй закон обычно считают самым полезным из трех, поскольку он позволяет нам рассчитать путь частицы через область, где действует сила. Там, где сила толкает сзади, мы ускоряемся в том же направлении; когда она толкает спереди, мы тормозимся. Если сила толкает сбоку, мы поворачиваем в том направлении, куда она вынуждает нас двигаться.
Сам закон записывается в форме:
Сила = масса ? ускорение,
где масса (более специальный термин — инерционная масса) является мерой сопротивления частицы действию силы. Для заданной силы ускорение велико, если масса мала, но если масса велика, то ускорение мало. Другими словами, высокая инерционная масса дает низкий уровень отклика, и наоборот. Острый глаз заметит тавтологию в этом законе, поскольку он определяет массу в терминах силы, а силу в терминах массы.
Поскольку ускорение является скоростью, с которой меняется скорость, мы можем, по-видимому, оценить по достоинству то, что внутри второго закона Ньютона зарыта возможность предсказания пути частицы, подвергающейся действию силы, которая может меняться от места к месту и принимать разные значения в разные моменты времени. «Зарыта» — термин, подходящий к этому случаю, поскольку расчет путей может оказаться весьма мудреным упражнением, более похожим на эксгумацию, чем на алгебру. Тем не менее это можно проделать для ряда простых случаев; но даже для сложных полей сил, таких, которые возникают возле двойной звезды, за эту задачу можно браться, используя компьютеры (рис. 3.2). Говоря короче, мы можем интерпретировать второй закон как утверждение, что, если мы знаем, где находится частица, или даже группа частиц, в данное время, мы можем в принципе предсказать, где ее найти и куда она будет двигаться в любое более позднее время. Предсказания таких точных траекторий представляют собой одно из достижений, прославивших классическую механику.
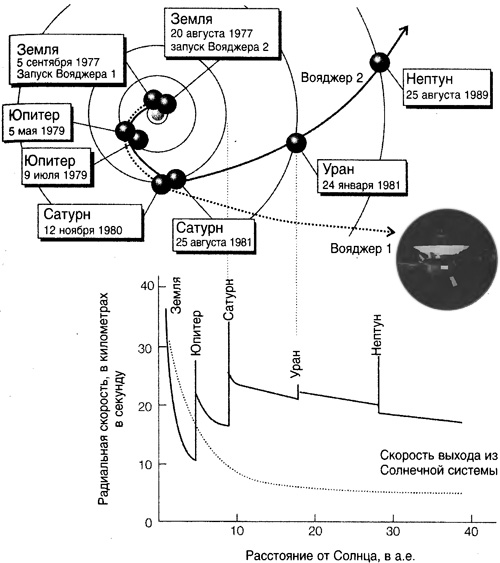
Рис. 3.2. Орбиты космических кораблей, рассчитанные с помощью механики Ньютона. Вычисления являются сложными, поскольку космические корабли подвергаются влиянию планет. Верхняя диаграмма показывает пути Вояджера 1 и Вояджера 2, начавших свои полеты в 1977 г. и функционирующих до сих пор. Вояджер 1, самый удаленный объект во Вселенной, сделанный человеком, покидает Солнечную систему со скоростью 3,6 а.е. в год (1 а.е., одна астрономическая единица представляет собой средний радиус орбиты вращения Земли вокруг Солнца и соответствует примерно 150 миллионам километров), под углом 35 градусов к плоскости планетарных орбит. Вояджер 2 также уходит из Солнечной системы со скоростью около 3,3 а.е. в год, под углом 48 градусов к этой плоскости, но в противоположном направлении. Нижний график показывает приращения скорости космических кораблей, когда они облетали каждую из планет. Эти поддержанные гравитацией приращения гарантируют, что скорость кораблей достаточна, чтобы они могли достичь своих целей, а затем покинуть Солнечную систему.
Третий закон Ньютона более глубок, чем выглядит. На первый взгляд кажется, что из него следует лишь то, что если бита прилагает силу к мячу, то мяч прилагает равную и противоположную силу к бите. Мы, разумеется, можем чувствовать силу, приложенную к мячу, когда мы ударяем по нему битой или пинаем его ногой. Однако подлинная значимость третьего закона состоит в том, что из него следует закон «сохранения». А сохранение это как раз та тема, которой посвящена вся эта глава, так что теперь мы начинаем подбираться к намеченной жертве. Однако сначала нам следует немного распаковать использованные здесь понятия.
Закон сохранения является утверждением, сообщающим о том, что ничто не меняется. Это может показаться самым неинтересным из возможных видов комментирования в науке. В действительности это, как правило, наиболее глубокий и наиболее содержательный тип научных законов, поскольку он дает интуитивное проникновение в симметрию — по существу, в форму — систем и даже в симметрии пространства и времени. Частным законом сохранения, следующим из третьего закона Ньютона, является закон сохранения импульса. В классической механике импульсом тела называется просто произведение его массы на его скорость:
Импульс = масса ? скорость.
Из этого определения следует, что быстро летящее пушечное ядро имеет большой импульс, а медленно летящий шарик пинг-понга имеет маленький импульс. Импульс является характеристикой силы удара движущегося тела при его столкновении с объектом, характеристикой той разницы, которую иллюстрирует сравнение ударов пушечного ядра и шарика для настольного тенниса. Закон сохранения импульса утверждает, что полный импульс системы частиц не меняется, если на систему не действует никакая внешняя сила. Поэтому, например, когда соударяются два бильярдных шара, их общий импульс после соударения остается таким же, каким он был до него. Прежде чем мы сможем понять это утверждение, нам придется более полно рассмотреть содержание понятия «импульс».
Импульс есть направленная величина, в том смысле, что две частицы одинаковой массы, движущиеся с одинаковой скоростью, но в разных направлениях, имеют разные импульсы. Два бильярдных шара, катящиеся друг к другу по одной прямой с одинаковой скоростью, имеют равные, но противоположно направленные импульсы, а их общий импульс равен нулю. Когда они сталкиваются «лоб в лоб», они останавливаются, так что импульс каждого мгновенно обращается в нуль, а общий импульс после столкновения снова равен нулю. Мы видим в этом примере, что, хотя импульсы отдельных частиц меняются, общий импульс остается неизменным. Это заключение обобщается на все случаи: какие бы импульсы ни имели индивидуальные частицы первоначально, сумма этих моментов (с учетом различных направлений и величин импульсов) после взаимодействия частиц будет оставаться такой же, какой была прежде (рис. 3.3). Бильярд как таковой является игрой, основанной почти полностью на принципе сохранения импульса: каждое столкновение шаров между собой или шара с бортом подчиняется этому закону и порождает различные траектории движения по столу, зависящие от первоначального угла подхода.
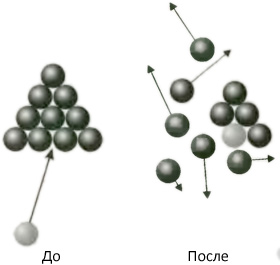
Рис. 3.3. Столкновения и взаимодействия в целом сохраняют импульс в том смысле, что полный импульс после столкновения остается таким же, каким он был в начале. Здесь мы видим столкновение шара с группой шаров. Импульс ударного шара указан с помощью длины и направления стрелки слева. Этот импульс передается шести «красным» шарам, и их индивидуальные импульсы заданы длинами и направлениями стрелок справа. Если вы сложите эти стрелки «головой к хвосту», не меняя их ориентации, вы получите в результате длину и направление начальной стрелки.
Теперь мы можем совершить гигантский, но контролируемый прыжок из бильярдной во Вселенную. Забавно, что, поскольку импульс сохраняется в любом процессе, величина импульса Вселенной тоже должна быть фиксированной. Поэтому, когда вы выезжаете в своем автомобиле, пусть даже вы всего лишь набираете импульс при разгоне или меняете направление вашего импульса, поворачивая за угол, что-то где-то получает импульс так, чтобы общий импульс Вселенной не изменился. Когда вы выезжаете, вы действительно немного толкаете Землю в противоположном направлении: вы ускоряете движение Земли по орбите, если трогаетесь в одном направлении, и замедляете, если отбываете в другом направлении. Однако масса Земли столь велика в сравнении с массой вашего автомобиля, что этот эффект будет совершенно незаметен, как бы много покрышек вы ни спалили. Но он существует.
Я упомянул ранее, что закон сохранения является следствием симметрии, или окном в симметрию, или что-то в этом роде. Что-то в этом роде в данном случае есть само пространство, так как в конечном счете симметрия пространства ответственна за сохранение импульса. Симметрия пространства, форма пространства: что это может означать? В данном примере все это означает, что пространство не состоит из кусков. Если вы двигаетесь сквозь пустое пространство по прямой линии, оно остается в точности тем же самым: повсюду оно гладкое и неизменное. Сохранение импульса это как раз знак того, что пространство не является кусковатым, а третий закон Ньютона это способ высказать то же самое на «высоком уровне».
Существует еще одно следствие третьего закона Ньютона, другой закон сохранения, другое интуитивное проникновение в форму пространства. Мы обсуждали импульс, характеристику частицы, движущейся по прямой линии. Существует еще одно свойство, момент импульса или момент количества движения, характеристика частицы, движущейся по кругу. Быстро вращающееся тяжелое маховое колесо имеет очень большой момент импульса, а медленно вращающееся колесо велосипеда имеет маленький момент импульса.
Момент импульса может быть передан от одного объекта другому, если первый объект прилагает ко второму вращающий момент, закручивающую силу, и отклик второго тела на этот вращающий момент зависит не только от его массы, но и от того, как эта масса распределена. Например, труднее разогнать колесо, если его масса сосредоточена в ободе, чем если та же масса расположена около оси. Вот почему в маховом колесе сталь сосредоточена около обода (рис. 3.4): такое распределение хорошо гасит изменения угловой скорости, а металл около оси менее эффективен и поэтому является излишним.

Рис. 3.4. Маховое колесо имеет значительную массу, сконцентрированную на большом расстоянии от его оси. Такое колесо требует большого вращающего момента (закручивающей силы), чтобы изменить свой момент импульса. В модели приводимого в движение паром тягового двигателя, показанной на иллюстрации, маховое колесо (верхнее из изображенных колес) помогает сохранять устойчивое движение поршня.
Если внешний вращающий момент к системе не прилагается, то момент импульса сохраняется. Предположим, что два вращающихся бильярдных шара соударяются на полированном столе; тогда момент импульса может быть передан от одного к другому и вращение одного может частично перейти к другому. Тем не менее момент импульса после столкновения остается таким же, каким он был первоначально: момент импульса сохраняется. То же верно и в целом: полный момент импульса семейства взаимодействующих частиц нельзя ни создать, ни уничтожить. Даже если вращающийся бильярдный шар замедляет движение из-за трения, момент импульса не теряется: он переходит к Земле. В результате Земля вращается немного быстрее (если бильярдный шар первоначально крутился в том же направлении, что и Земля) или немного медленнее (если шар вращался в противоположном направлении). Если вы едете в направлении вращения винта по северному полушарию, вы ускоряете вращение Земли, но замедляете его снова, если тормозите или останавливаетесь. Вселенная в целом, очевидно, имеет нулевой момент инерции, поскольку не существует никакого вращения Вселенной как целого. Таким он и будет оставаться всегда, поскольку мы не можем производить момент инерции; мы можем лишь переносить его от одного кусочка Вселенной к другому.
А что же говорит нам сохранение момента импульса о форме пространства? Поскольку момент импульса является характеристикой вращательного движения, мы можем подозревать, что его сохранение говорит нам, какую форму пространство имеет, когда мы вращаемся. Действительно, закон сохранения момента импульса показывает, что если мы движемся по кругу вокруг некоторой точки, то мы не обнаружим в пространстве никаких кусков. Сохранение импульса возникает из однородности пространства при движении по прямой линии; сохранение момента импульса возникает из однородности пространства при движении по кругу. Более технически выражаясь, сохранение импульса говорит нам о том, что пустое пространство гомогенно, а сохранение момента импульса говорит нам о том, что оно изотропно. Третий закон Ньютона сообщает нам то, что мы можем считать очевидным: это пространство однородно для нашего движения (пока на нас не действуют внешние силы или вращающие моменты). Однако тот факт, что этот закон имеет измеряемые следствия, означает, что наше умозрение в кресле о природе пространства открыто для экспериментальной проверки, и это замечательно.
Вы могли заметить, что энергия пока не играла роли в нашем обсуждении. Ньютон не использовал этот термин и умер за век до того, как Юнг предложил принять его. Его формулировка механики, при всей ее оригинальности и элегантности, была, по существу, физикой фермерского двора (или, точнее, физикой ледового катка), использующей почти буквально осязаемую концепцию силы. Вы и я, как мы думаем, точно знаем, что такое сила, поскольку мы знаем, когда мы прилагаем ее или испытываем ее действие. То, что Ньютон принял ее в качестве центральной концепции своей механики, и означает, что физика едва отъехала с фермерского двора. Как мы видели на примере Галилея, достижение прогресса в науке обычно сопровождалось переходом от осязаемого к абстрактному, и вследствие этого понимание предмета становилось глубже. Имеется много сундуков с одеждой, но важен один определяющий ее человеческий скелет: если мы поймем скелет, мы поймем много больше, чем поняли бы, осмотрев развешенные одежды. Введение энергии знаменует появление в физике абстракции, осветившей мир своим необычайным светом.
Этому свету потребовалось полвека на то, чтобы осветить мир. В начале девятнадцатого века энергия еще была литературным термином; к середине века энергия оказалась в плену у физики. Ее окончательное принятие может быть датировано с определенной точностью, поскольку в 1846 г. Уильям Томсон (1824-1907, с 1892 г. лорд Кельвин) еще мог написать, что «физика есть наука о силе», но в 1851 г. он провозглашал, что «энергия есть первичный принцип». Этот переход был совершен в два этапа: сначала изучение движения частиц (включая частицы, которые мы считаем планетами), а затем изучение действия сложного собрания частиц, называемого паровым двигателем.
Для частиц рассвет начался серией из вспышек света в первые годы девятнадцатого столетия. Сначала, как мы видели, Томас Юнг предложил использовать термин энергия для величины, получаемой умножением массы частицы на квадрат ее скорости. Эта энергия движения понималась как мера vis viva, или живой силы, и рассматривалась как разумная мера силы в событиях, происходящих в системе частиц. Парадоксально: чем больше живая сила у пушечного ядра, тем больше смертей и разрушений оно может произвести.
Определение энергии выражением масса ? скорость2, данное Юнгом, было не совсем правильным. Он пришел к своему предположению, рассматривая силу, которую движущийся объект прилагает к чему-нибудь при столкновении с ним, и понимая, хотя и не вполне четко, что сила, прилагаемая данным телом, возрастает в четыре раза, если скорость удваивается. Это верно, но численный множитель в выражении Юнга неправилен. Он осознал свою ошибку примерно в 1820 г., когда понял, что концепцию работы (которую мы обсудим ниже) можно скомбинировать со вторым законом Ньютона и вывести отсюда, что энергия, связанная с движением, лучше выражается половиной этой величины. Некоторое время эту величину называли актуальной энергией, но название быстро сменилось на кинетическую энергию, и этот термин используется теперь везде. Итак
Кинетическая энергия = 1/2 ? масса ? скорость2.
Таким образом, быстро движущееся тяжелое тело имеет большую кинетическую энергию, в то время как медленно движущееся легкое тело имеет маленькую кинетическую энергию. Падающий шар приобретает кинетическую энергию, поскольку он ускоряется. В отличие от импульса, кинетическая энергия одинакова при любом направлении движения частицы: шар, двигающийся горизонтально с заданной скоростью, имеет одну и ту же кинетическую энергию независимо от направления движения, а его импульс различен для разных направлений.
«Работа», на которую мы ссылались, является решающей концепцией для изучения энергии и заслуживает немедленного разъяснения. Мы должны понимать, что то, что ученые имеют в виду под этим названием, не вполне то же самое, что повседневное значение слова «работа». В науке работа совершается, когда объект преодолевает силу, действующую в направлении, противоположном его движению. Чем дальше мы продвигаем объект, тем больше работа, которую нам приходится совершить. Чем больше противодействующая сила, тем больше работа, которую нам приходится совершить. Поднятие тяжелого объекта, движение против силы притяжения к Земле (противодействующей силы, поскольку она препятствует движению груза вверх) требует совершения большой работы. Поднятие со стола листа бумаги также требует работы, правда не очень большой. Поднятие того же объекта на такую же высоту на Луне, где притяжение меньше, требует совершения меньшей работы, чем на Земле.
Поднятие металлического блока с преодолением гравитационной силы представляет больший интерес, чем можно подумать. Сначала вообразим чурбан на катке, блок, который толкают по отполированной поверхности без трения. Блок ускоряется, пока мы продолжаем его толкать. В результате его кинетическая энергия будет возрастать от нуля вначале до той величины, которую мы изберем, или до того момента, когда мы упадем в изнеможении и перестанем прикладывать силу, а блок начнет ускользать от нас по льду с постоянной скоростью. Работа, которую мы проделали, превратилась в энергию, энергию движения. (Множитель 1/2 в выражении для кинетической энергии был введен для того, чтобы гарантировать, что две эти величины, работа и кинетическая энергия, равны.) Теперь мы можем обратить это рассуждение, допустив, что блок движется равномерно по нашему галилеевскому столу без трения и ударяется о некое хитроумное приспособление, способное преобразовать его движение в поднятие груза (рис. 3.5). Вся кинетическая энергия превращается в работу, в го же количество работы, которое мы затратили для первоначального разгона блока.

Рис. 3.5. Движение тела можно использовать для того, чтобы произвести работу, поэтому ему соответствует форма энергии, известная как кинетическая энергия. В данном примере шар ударяет по поршню, а движение поршня преобразуется с помощью ряда приспособлений в поднятие груза, представленного другим шаром. Работа, проделанная при поднятии второго шара (пропорциональная его весу и высоте, на которую шар поднят), равна кинетической энергии катящегося шара.
Эти наблюдения дают возможность ввести следующее определение: энергия есть способность произвести работу. Это и в самом деле все, чем она реально является. Где бы вы ни встретили термин энергия, использованный в техническом, а не в литературном смысле, он всегда означает способность произвести работу. Большое количество запасенной энергии (быстро движущаяся тяжелая масса) может в принципе произвести много работы, поднять тяжелый груз на большую высоту. Объект, обладающий лишь небольшим количеством энергии (медленно движущаяся легкая масса), может произвести лишь малое количество работы, поднять легкий груз лишь на маленькую высоту. При удвоении скорости объект учетверяет работу, для выполнения которой его можно запрячь.
Сделаем теперь следующий шаг. Предположим, что мы поднимаем груз на определенную высоту и прикрепляем его к системе блоков, которая может поднимать другой груз (рис. 3.6). Когда мы отпускаем первый груз, он поднимает второй. То есть он производит работу. Таким образом, первый груз имеет возможность произвести работу, даже несмотря на то, что вначале он был неподвижен. Это значит, что он обладает энергией. Эта форма энергии, которой частица обладает благодаря определенному положению, называется потенциальной энергией. Термин ввел в оборот в 1853 г. Уильям Макуорн Рэнкин (1820-72), один из основателей науки об энергии, которому предстоит снова появиться в этом повествовании.

Рис. 3.6. Даже если объект неподвижен, он может все же обладать энергией благодаря своему положению: эта форма энергии известна как потенциальная энергия. Слева тяжелый груз готов к опусканию. Справа тяжелый груз опустился на платформу, и в процессе этого был поднят легкий груз. Таким образом тяжелый груз совершил работу, и поэтому он должен был обладать энергией с самого начала. Эта энергия и была его начальной потенциальной энергией.
На этом этапе мы видим, что существуют две формы энергии, кинетическая энергия (способность производить работу благодаря движению) и потенциальная энергия (способность производить работу благодаря положению). Хотя вы будете часто встречать термины типа «электрическая энергия», «химическая энергия» и «ядерная энергия», таких вещей на самом деле нет: эти термины являются просто удобными сокращенными терминами для специальных и частных комбинаций кинетической и потенциальной энергий. Электрическая энергия является главным образом потенциальной энергией отрицательно заряженных электронов в присутствии положительных зарядов. Химическая энергия устроена несколько более сложно, но ее можно проследить до потенциальной энергии электронов в молекулах и кинетической энергии их движения, когда они выходят за пределы молекулы. Ядерная энергия устроена аналогично, но возникает из взаимодействий и движений субатомных частиц внутри атомного ядра. Исключением из универсальности терминов «кинетическая и потенциальная энергии» является энергия электромагнитного излучения (например, энергия света, приходящего к Земле от Солнца и согревающего нас или производящего для нас пищу посредством фотосинтеза). Но что это касается энергии, запасенной в веществе, то она полностью состоит из кинетической и потенциальной энергий. Итак, на данный момент, мы действительно поняли все, что требуется знать об энергии.
Ну, не совсем все. Всего мы еще не знаем, как вы можете судить по числу страниц в этой главе, еще не прочитанных вами, и тому факту, что другие главы тоже развивают концепцию энергии. Энергия заслуживает всего этого пространства текста, потому что она является центральным понятием для Вселенной, для всех ее структур и событий. В самом деле, двумя великими основаниями науки являются причинность, влияние одного события на события последующие, и энергия. Причинность есть по существу связность и согласованность цепочки команд, поддерживающей движение во Вселенной, которую мы распутываем, чтобы достичь понимания; энергия всегда бдительно стоит на страже приличий, гарантируя, что причинность будет производить лишь допустимые действия. Как мы увидим дальше, энергия есть поистине конвертируемая валюта космической бухгалтерии.
Давайте подробнее рассмотрим понятие энергии. Потенциальная энергия является потенциальной потому, что ее можно конвертировать в vis viva, действующую энергию, кинетическую энергию. Предположим, мы обрезаем шнур, удерживающий груз на высоте. Он срывается вниз (мы действуем на Земле, в земном гравитационном поле) и ускоряется при падении. В момент, предшествующий его удару о землю, он приобрел много кинетической энергии и утратил всю свою потенциальную энергию. Он все еще имеет возможность совершить работу. С помощью устройства, спроектированного подходящим образом, мы можем уловить эту кинетическую энергию, позволив падающему грузу ударить по рычагу, который подбросит другой груз вверх, подобно старинному ярмарочному аттракциону для силачей, когда ударом молота по рычагу отправляли груз вверх по направлению к колоколу (рис. 3.7). Разумеется, такой аттракцион является прекрасным конспектом основного содержания этой главы. Мы должны заключить, что потенциальная энергия и кинетическая энергия беспрепятственно взаимно конвертируются.

Рис. 3.7. В этой абстрактной схеме ярмарочной машины «испытай свою силу» кинетическая энергия груза, падающего слева, заставляет подняться вверх шар справа. Кинетическая энергия падающего груза (возможно, молота) превращается в работу по поднятию шара.
Из эксперимента, который мы проделали, также следует, что полная энергия, сумма потенциальной и кинетической энергий первого груза, является постоянной. Таким образом, мы приходим к сохранению энергии, к наблюдению, что энергия никогда не может возникнуть или уничтожиться, что полная энергия неизменна. Это заключение может быть формально доказано с помощью второго закона Ньютона, так что по смыслу этот закон является утверждением о сохранении энергии, точно так же, как третий закон есть завуалированное утверждение о сохранении импульса.
Два других закона сохранения, с которыми мы столкнулись (законы сохранения импульса и момента импульса), были связаны с симметрией и говорили нам нечто о форме пространства. Теперь на ум приходит очевидный вопрос, не является ли сохранение энергии следствием симметрии, и если да, то какой? В главе 9 мы увидим, что нужно думать не о пространстве в отдельности, а о пространстве-времени, а времени необходимо предоставить равные права с пространством. Нам, возможно, удастся почувствовать, что, в то время как сохранение импульса произрастает из формы пространства, сохранение энергии происходит из формы времени. Это действительно именно так, тот факт, что энергия сохраняется, является следствием того факта, что время не кусковато: оно гладко простирается из прошлого в будущее без сплющенных или растянутых участков. Связь между законами сохранения и пространством-временем столь глубока, что законы сохранения выживают, даже когда ньютоновские законы движения рушатся, ибо сохранение импульса и энергии остаются в целости в релятивистской и квантовой механиках.
Поскольку второй закон Ньютона является по существу утверждением о сохранении энергии, мы можем видеть, что этот закон является прямым следствием гладкости времени, также как третий закон является прямым следствием гладкости пространства. Такое объяснение большинство ученых считают сегодня более убедительным, чем пылкий религиозный энтузиазм Томсона и многих его современников, считавших сохранение энергии следствием щедрости Бога. Бог, утверждали они, одарил мир энергией, и эта энергия, будучи божественной, не может ни уменьшиться от человеческого вмешательства, ни быть уничтоженной никакими нашими действиями.
Анализ поведения частиц в терминах кинетической энергии, потенциальной энергии и сохранения энергии превратил энергию в конвертируемую валюту физики в 1867 г. вследствие публикации авторитетного труда Томсона и Тейта «Курс натуральной философии». К тому времени уже возникло понимание, что концепция энергии помогает свести воедино все части физики. Так в 1847 г. ученый-универсал Герман фон Гельмгольц (1821-94) использовал эту концепцию, чтобы показать внутреннее единство механики, света, электричества и магнетизма. Но несмотря на этот успех, существовала докучная проблема, которая угрожала всему сооружению, проблема тепла.
Тепло долго было таинственным явлением, до тех пор, пока разработка парового двигателя и зависимость от него национальных экономик, а следовательно, успех в войне и торговле, не выдвинули его в центр внимания науки. Проблема, однако, была не только в том, что природа тепла была неизвестна, но и в том, что этот вопрос, казалось, лежал за пределами достижений современной физики.
Долгое время многие считали, что тепло является жидкостью, которой даже дали название теплород (или калорик, от латинского color, тепло), одной из тех «неощутимых», невесомых жидкостей, которые так любили ранние исследователи. Теплород был не только неощутимым (и, следовательно, очень удобно недоступным для обнаружения путем взвешивания), он также был «тонким», в том смысле, что везде мог проникать, даже между телами, плотно сомкнутыми вместе. Мы можем посмеиваться над этими ложными представлениями, но и сегодня не каждый может объяснить, что такое «тепло», и более того, лексика, связанная с теплородом, все еще пропитывает повседневный язык: мы говорим о тепле, текущем, как жидкость, от горячего тела к холодному.
Теплород изгнал из науки в 1798 г. ученый, изобретатель, политик, бабник, солдат, святоша, государственный муж, реформатор и шпион Бенджамин Томпсон, граф Румфорд (1753-1814). Томпсон родился в Массачусетсе, бежал в Англию в 1776 г., основал в 1799 г. Королевское общество и переехал в Баварию, где был назначен военным министром, министром внутренних дел, гофмейстером двора, статским советником и графом Священной Римской империи. Он выбрал себе титул по имени города Румфорд (позже Конкорд) в Нью-Гемпшире, где родилась первая из его жен. Изгнание теплорода произошло в результате наблюдений Румфорда за рассверливанием ствола пушки, который он курировал в мюнхенском арсенале. Он записал:
18,77 фунта воды в дубовой бочке. В начале 60° F; после того как две лошади крутили станок 2? часа, вода закипела.
Он заключил из этого и подобных экспериментов, что тепло могло производиться постоянно и было неистощимо. Если так, то оно должно было производиться трением, и поэтому его нужно рассматривать скорее как движение частиц, обрабатывающих металл пушки, чем как жидкость, скрытую в металле.
Предстоял еще долгий путь до того момента, когда тепло количественно вошло в научный обиход, была определена его атомная природа и оно было включено в закон сохранения энергии. Потребность понять тепло вырастала, как мы указали, из огромной важности парового двигателя в промышленности, и неудивительно, что большинство результатов, которые привели к нашему современному пониманию тепла, было получено группой ученых, сосредоточенной на севере Британии, в Глазго и Манчестере, и имевшей тесные связи с индустрией мануфактур.
Есть одна тема, которая будет вновь и вновь возникать на протяжении всей этой книги, и это тема о том, что продвижение науки связано с упразднением универсальных констант. Здесь появляется первый проблеск того, в чем она заключается, и прояснение того, что из этого вытекает. В девятнадцатом веке (и, следует признать, в некоторых частях мира в двадцать первом) работа измерялась одним набором единиц (единицей оказался эрг, но детали здесь не важны), а тепло измерялось другим набором (калории). Различие единиц измерения этих двух величин скрывало тот факт, что эти величины по существу одно и то же. В девятнадцатом веке прилагалось много усилий в попытке измерить «механический эквивалент тепла», работу, которая может быть получена из данного количества тепла, и найти эффективный коэффициент перехода от калорий к эргам. Эти усилия дали существенный вклад в прогресс науки и экспериментальные обоснования для закона сохранения энергии. Однако, с нашей сегодняшней точки зрения, это была пустая трата времени. Не поймите меня неправильно: это была плодотворно пустая трата времени. Она была плодотворной, поскольку помогла показать, что тепло есть форма энергии, что невозможно произвести работы больше, чем запасено тепла, и что тепла производится не больше, чем произведено работы. Это была пустая трата времени лишь потому, что теперь мы понимаем работу и тепло как две формы одной целостности, энергии, измеряем их одними и теми же единицами и больше не нуждаемся в переводе одной единицы в другую.
Джеймс Джоуль (1818-89) является тем, кто заслуживает наибольшего уважения за исключительно плодотворную пустую трату времени. Джоуль, рожденный в Манчестере, сын богатого пивовара, имел достаточно собственных средств, чтобы проводить исследования до тех пор, пока около 1875 г. деньги не кончились. В своем знаменитом эксперименте Джоуль использовал быстро вращающиеся гребные колеса, приводимые в движение падающим грузом и баламутящие воду, и измерял подъем температуры воды (рис. 3.8). Таким способом он сумел показать, что работа может быть преобразована в тепло. Сравнивая работу, необходимую, чтобы увеличить температуру воды на заданную величину, с количеством тепла, нужным для того, чтобы достичь того же эффекта, он смог измерить механический эквивалент теплоты. Хотя он и измерял величину, которая ныне бесполезна, он заслуживает безмерных похвал за то, что установил эквивалентность тепла и работы и таким образом показал, что эта величина, на попытки измерения которой он потратил так много времени, не была важной. Для увековечения памяти о его вкладе единица, которой измеряются работа, тепло и, конечно, энергия в целом, названа джоулем. Джоуль (Дж) очень маленькая единица энергии: каждый удар человеческого сердца производит работу около 1 Дж. Каждый день, в соответствии приблизительно со ста тысячами ударов, ваше сердце производит около ста тысяч джоулей работы, гоня кровь по вашему телу, поэтому вам необходимо поглощать достаточно пищи, чтобы обеспечить количество энергии, достаточное для поддержания его тикания. (Думание об этом требует немного больше энергии.)

Рис. 3.8. Идеализация прибора Джоуля для измерения механического эквивалента теплоты. Падающий груз вращает лопасти в воде, помещенной в изолированный контейнер. Проделанная работа может быть вычислена с помощью высоты, на которую опускается груз. Отслеживается температура воды, и величина поднятия температуры затем используется, чтобы вычислить количество теплоты, необходимое для достижения того же эффекта.
Работы Джоуля и его современников без сомнений установили, что работа и тепло являются формами энергии и что после принятия их в расчет балансовый отчет энергии остается неизменным. Доказано, что энергия сохраняется даже в грохочущих машинах, которые жили за счет тепла и фыркали паром, не говоря уже о более простых системах частиц, составляющих тела, рассматриваемые ньютоновской динамикой.
Очевидная универсальная справедливость закона сохранения энергии исключает возможность построить когда-нибудь вечный двигатель. Вечный двигатель является прибором, который производит работу, не поглощая горючее. То есть он создает энергию. Энергия жуликов, однако, судя по всему, вечна, и все виды фантастических машин по-прежнему демонстрируются и неизменно, после анализа или просто разбирания на части, оказываются надувательством. Мы так уверены, что энергия сохраняется, что ученые (и патентные бюро) больше не рассматривают серьезно заявления об опровержении этого факта, и поиск вечного движения сегодня считается занятием чудаков.
Хотя тепло и работа являются двумя ликами энергии, между ними, как и предполагает здравый смысл, имеется разница. Полное понимание тепла и работы, и того, каким образом они выражают энергию, придется отложить до развития молекулярного понимания этого определения. И, как это часто бывает в науке, вместе с пониманием приходит осознание того, что таких вещей не существует: нет такой вещи, как тепло и нет такой вещи, как работа! Поскольку очевидно, что мы в нашей повседневной жизни просто окружены обоими, это замечание заключает в себе больше, чем кажется с первого взгляда. Давайте вникнем в это.
Во-первых, что я имею в виду, когда утверждаю вещь, очевидно парадоксальную и противоречащую всему, что было сказано прежде: ни тепло, ни работа не есть формы энергии? Ключевым пунктом здесь является то, что оба явления являются путями переноса энергии из одного места в другое. Работа есть один путь переноса, тепло — другой. Нет такой вещи, как «работа», запасенная в двигателе и высвобождаемая, когда мы едем по дороге или поднимаем груз. В точности так же (хотя это и противоречит тому, что мы используем этот термин в легкомысленных разговорах) не существует такой вещи, как «тепло», запасенное в объекте, несмотря даже на то, что мы можем думать об объекте, как о горячем. Тепло — это способ переноса энергии: это энергия в переходе, а не энергия, которой что-то обладает. Возможно, вы уже можете уловить, что, коль скоро я разъясняю, как именно вам следует понимать термин «тепло», вам следует отринуть все прежние понятия, основанные на неточных терминах повседневной речи. Чтобы создать новый термин, ученые часто выбирают знакомое слово, срезают с него мясо и жир и используют лежащую под ними кость. И так же часто ученые совершенствуют язык, чтобы он не был замкнутым в себе и холодным, и даже отбивают хлеб у поэтов, но они ведь действительно знают о чем идет речь.
Более 800 000 книг и аудиокниг! 📚
Получи 2 месяца Литрес Подписки в подарок и наслаждайся неограниченным чтением
ПОЛУЧИТЬ ПОДАРОКЧитайте также
ГЛАВА ТРЕТЬЯ. ЩЕДРАЯ ОСЕНЬ
ГЛАВА ТРЕТЬЯ. ЩЕДРАЯ ОСЕНЬ Грибы, костяника,княженика, морошка,вороника, брусника,клюква, калина, рябинаобыкновенная, облепиха,крушиновидная, лимонниккитайский, шиповникмайский, лещина,орех грецкий, кедрсибирскийи другие. Глава третьяМеняется лес в предосеннюю пору.
Глава третья С деревьев на землю
Глава третья С деревьев на землю Важнейшие события оказываются непреднамеренными; случайность обращает ошибки во благо… Величайшие мировые события не готовятся умышленно, они происходят сами собой. Георг К. Лихтенберг
Глава третья. Синоптики природы
Глава третья. Синоптики природы Проблема точного прогнозирования погоды - одна из самых древних, она так же стара, как и само человечество. Потребность в какой-то мере предвидеть погоду появилась у человека с переходом его к оседлой жизни, к занятию земледелием и
Глава третья. Взгляды креационистов
Глава третья. Взгляды креационистов Креационисты отвергают научные методы и данные.Сторонники идей, известных под общим названием «креационизм», а в последнее время также «концепция разумного замысла», придерживаются весьма разнообразных взглядов. Креационистами (в
Глава третья: Открытия XX столетия
Глава третья: Открытия XX столетия Все еще неведомая Африка… Возможны ли открытия живых существ, неведомых науке, в нашем столетии, когда в глубины океана опускаются батискафы, в космос летают ракеты, а средства массовой информации связывают всех людей, несмотря на
Глава третья. ПТИЦА, КОТОРАЯ ИСЧЕЗАЛА
Глава третья. ПТИЦА, КОТОРАЯ ИСЧЕЗАЛА А долина все уже и уже… А вечер все холодней и темней… «Охота Ворчуна» В 1948 году в Новой Зеландии было сделано открытие, которое потрясло мир орнитологов и пробудило его от обычной спячки, а именно была открыта (точнее, вновь открыта)
Глава третья Выращивание потомства
Глава третья Выращивание потомства У голой обезьяны родительское бремя тяжелее, чем у любого другого животного. Если кто и может состязаться с нами в этом отношении, то в категориях интенсивности, но только не экстенсивности. Прежде чем оценить значение этой тенденции,
Глава третья О преломлении
Глава третья О преломлении Подобно тому, как явления отражения были объяснены волнами света, отраженного от поверхности гладких тел, подобно этому прозрачность и явления преломления мы объясним при помощи волн, распространяющихся внутри и через прозрачные тела, будь то
Глава третья Там, где не ступала нога человека
Глава третья Там, где не ступала нога человека Машина времени и чудеса киноНа одной из московских киностудий сделали фильм о жизни растений. Самые удивительные, казалось, недоступные глазу человека тайны растений открываются на экране.В землю падает крошечное семечко.
Глава 6 Кундалини: спящая космическая энергия внутри человека
Глава 6 Кундалини: спящая космическая энергия внутри человека Основная сущность пранаямы – это очищение Нади, чувствительных нервов в нашем астральном теле, заряжаемых потоком праны. В терминах науки о физиологии дыхания это может быть истолковано как функция
Глава третья
Глава третья Поощряемый Спенсером Кертисом Брауном, Даррел сел писать вторую книгу, посвященную путешествию в Британскую Гвиану. Спенсер весьма разумно посоветовал Джерри подготовить ее, не дожидаясь выхода «Перегруженного ковчега», дескать, если первая книга станет
Глава третья Ливер и столкновение мнений
Глава третья Ливер и столкновение мнений Почему мы едим одно и отвергаем другое?«Комплект образцов традиционного питания северных народов и источников поддержания здоровья» включает подборку из 48 фотографий, снабженных пояснительными подписями. На этих иллюстрациях