Глава 4 Геномика, системная биология и универсалии эволюции: эволюция генома как феномен статистической физики

We use cookies. Read the Privacy and Cookie Policy

Глава 4

Геномика, системная биология и универсалии эволюции: эволюция генома как феномен статистической физики

Пер. К. Муратовой

В предыдущей главе была подчеркнута относительная стабильность отдельных генов, составляющая яркий контраст динамизму геномной эволюции. Если гены или домены принять за атомарные единицы геномной эволюции, тогда геномы можно рассмотреть как статистические ансамбли таких единиц. Мы можем продолжить эту очень упрощенную, но очевидно не бессмысленную и потенциально продуктивную физическую аналогию и рассмотреть геномы как структуры, подобные газу или жидкости, в которых силы межмолекулярного взаимодействия хоть и являются важными параметрами, но слабы по сравнению с внутримолекулярными взаимодействиями (лежащими в основе стабильности молекул), в отличие от твердых тел, в которых межмолекулярные взаимодействия сильны и имеют определяющее значение.

Из статистической физики известно, что поведение ансамбля слабовзаимодействующих частиц (молекул) следует простым и универсальным статистическим закономерностям, таким как распределение Больцмана для скоростей частиц. Аналогия между ансамблями генов (геномами) и ансамблями молекул (газами и жидкостями) наталкивает нас на поиск статистических закономерностей в функционировании и эволюции генома. Более того, размышляя таким образом, мы можем с некоторой степенью уверенности предположить, что эти статистические закономерности должны представлять собой математически простые, универсальные законы распределения значений определенных параметров, описывающих процесс эволюции. Мы убедимся в этой главе, что поиск таких эволюционных универсалий — дело далеко не безнадежное.

Перед обсуждением статистических свойств генных ансамблей необходимо обратить внимание на еще одно ведущее направление биологических исследований первой декады третьего тысячелетия, представляющее собой новую область науки, часто называемую, может быть не очень удачно, системной биологией. Системная биология провозглашает своей конечной целью построение моделей и понимание функционирования биологических систем во всей их сложности. Реальное положение дел на данном этапе становления этой области исследований заключается в том, что основное внимание направлено на агрегацию обширных данных специфического типа, таких как транскриптомы (совокупность всех экспрессируемых РНК клетки, ткани или организма), протеомы (совокупность всех экспрессированных белков), метаболомы (совокупность всех метаболитов) и другие «-омы» (Bruggeman and Westerhoff, 2007; Koonin and Wolf, 2008a). Все эти «-омы» описываются системной биологией с помощью количественных понятий, таких как концентрация белка или метаболита.

Так же как и генетику в ее первые годы, системную биологию многие ученые приняли за скучную «большую науку» и слишком хлопотливое занятие. (Подозреваю, что это отношение до сих пор преобладает.) Так же как и с генетикой, первый взгляд оказался, мягко говоря, недальновидным. Наличие высококачественных данных по генной экспрессии, генетическим и белок-белковым взаимодействиям, локализации белка в клетке и других данных системного уровня в масштабе генома открыло новые измерения эволюционного анализа (иначе иногда называемого эволюционной системной биологией) и обеспечило его взаимопроникновение с эволюционной геномикой. В исследованиях системной биологии, в масштабах генома, уже были открыты нетривиальные связи между эволюцией генных последовательностей, генной экспрессией, структурой белка и другими характеристиками генов и белков. Эти открытия в целом оказались совместимыми с точкой зрения на геном как на статистический ансамбль генов и дали возможность в новом свете рассмотреть селективную и нейтральную составляющие эволюции структуры и функций генома.

Взаимосвязь между эволюционными и фенотипическими параметрами, универсалии эволюции генов, белков и геномов и физическая модель эволюционного процесса

В предыдущей главе было показано, что белок-кодирующие гены (по крайней мере в отношении мутационных замен, приводящих к изменению аминокислот в кодируемом белке) принадлежат к числу наиболее консервативных последовательностей генома. Однако уже на раннем этапе исследований в молекулярной эволюции стало понятно, что скорости эволюционирования белок-кодирующих генов могут очень сильно разниться (Wilson et al., 1977). Этот широкий разброс значений в общем объясняли существованием широкого спектра функций белка, которые по-разному ограничивают скорость эволюции соответствующих генов. В самом деле, кажется само собой разумеющимся, что огромная роль ДНК-полимеразы, сложнейшего фермента, который катализирует встраивание комплементарных матрице нуклеотидов в растущую цепь ДНК, требует значительного ограничения на скорость эволюции для соответствующей ей генной последовательности, в то время как, например, для структурного белка, чья единственная задача состоит в поддержании целостности ядерного матрикса, такого сильного ограничения не требуется. Фундаментальное представление о том, что эволюция белок-кодирующих генов может сводиться не только к уникальным особенностям молекулярной структуры и функции белков, возникло уже на этом раннем этапе. В богатой идеями обзорной статье, опубликованной Аланом Вильсоном и коллегами в 1977 году, выдвигается гипотеза о том, что скорость эволюции генных последовательностей зависит как от уникальных функций кодируемого белка, так и от важности этого белка для выживания организма (Wilson et al., 1977). Однако в то время не было прямых способов изучения эволюционных ограничений, так что эти идеи, хоть и интригующие, тогда находились всецело в области умозрительных построений.

В начале третьего тысячелетия геномика и системная биология полностью преобразили область эволюционных исследований. Доступность множества данных по геномным последовательностям позволила проанализировать и сравнить распределения скоростей эволюции для полных наборов ортологичных генов в различных таксонах, а также изучить взаимосвязи скоростей эволюции ортологов в различных эволюционных линиях. Значения скоростей эволюции по несинонимичным сайтам в ортологичных генах могут различаться на три-четыре порядка, и это распределение значений гораздо шире, чем распределение скоростей по синонимичным сайтам. Замечательно, что формы графиков распределений по ортологичным белкам исключительно похожи, практически одинаковы для всех изученных клеточных форм жизни, от бактерий и архей до млекопитающих (см. рис. 4-2; Grishin et al., 2000; Wolf et al., 2009). Все эти распределения имеют так называемую логарифмически нормальную форму, то есть распределение логарифма эволюционной скорости близко к нормальному (распределению Гаусса, функция плотности вероятности которого имеет колоколообразную форму). В теории случайных процессов такая форма обычно представляет собой результат произведения многих независимых случайных величин. Универсальность функции распределения среди различных организмов, обладающих глубокими различиями в функциональной организации и сильно различающихся по размеру геномов, представляется неожиданной и может указывать на существование фундаментальных, простых объяснений, которые мы и обсудим в этой главе.

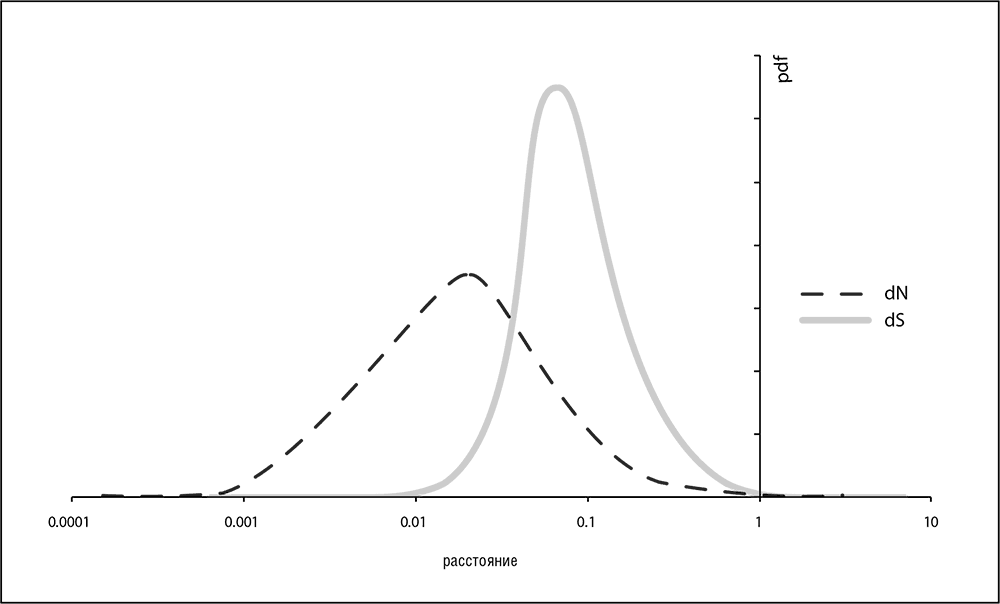
Рис. 4-1. Распределения скорости эволюции по несинонимичным и синонимичным сайтам в ортологичных генах человека и мыши: dN = скорость эволюции по несинонимичным сайтам; dS = по синонимичным; pdf = функция плотности вероятности. Данные из Wolf et al., 2009; для расчетов использовался пакет PALM (Yang, 2007)

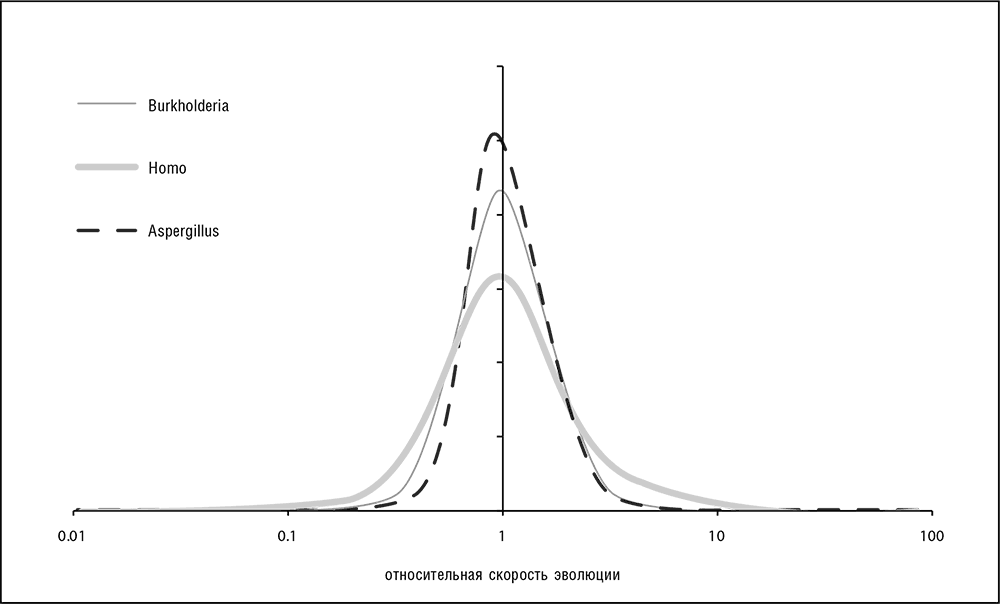
Рис. 4-2. Распределения скорости эволюции в наборах ортологичных генов бактерий и эукариот; Burkholderia = распределения для ортологов Burkholderia cenocepacia и Burkholderia vietnamiensis (протеобактерия); Homo = для ортологов человека и макаки-резус (приматы). Aspergillus = для ортологов Aspergillus fumigatus и Neosartorya fischeri (аскомицеты). Данные из Lobkovsky et al., 2010; для расчетов использовался пакет PALM (Yang, 2007)

Прогресс в системной биологии позволил измерить корреляции между скоростью эволюции и всеми возможными молекулярно-фенотипическими величинами, такими как уровень экспрессии, концентрации белков, белок-белковые взаимодействия, фенотипический эффект генной мутации и другими (Koonin and Wolf, 2006). Эти поиски корреляций стали практически самостоятельной областью исследований, цель которых, однако, состоит не в описании самих корреляций, а в построении физически осмысленной модели эволюции геномов и феномов. Было найдено много важных корреляций, что позволило увидеть существование некоторых закономерностей, несмотря на «зашумленность» молекулярно-фенотипических данных (особенно данных, полученных на ранних этапах исследований). На рис. 4-3 представлена простая и наглядная, хоть и неизбежно упрощенная общая картина результатов исследований (Wolf et al., 2006). Обобщение результатов показывает, что существуют два обширных класса переменных:

1. Интенсивные, эволюционные переменные — различные скорости геномных изменений, включая эволюцию последовательностей, потерю гена, перестройку генома и другие виды эволюционных процессов.

2. Экстенсивные, фенотипические переменные — скорость экспрессии, скорость трансляции, концентрация белка, частота взаимодействия с другими изучаемыми объектами.

Корреляции внутри каждого из двух классов обычно положительные, а корреляции между двумя классами — отрицательные (рис. 4-3). Эта закономерность предполагает модель «статуса генов», в которой высокостатусные гены эволюционируют медленно, имеют высокий уровень экспрессии и взаимодействуют со многими другими генами. Гены с низким статусом меняются быстро и имеют низкий уровень экспрессии и меньшее число партнеров (рис. 4-4).

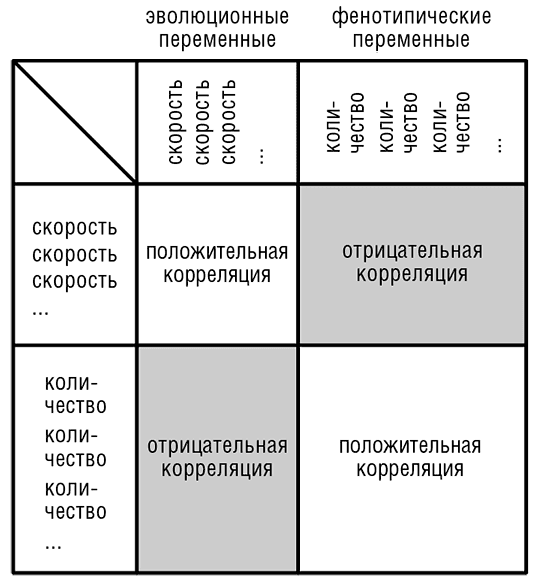
Рис. 4-3. Схематическая обобщенная картина корреляций эволюционных и молекулярно-фенотипических переменных.

Сильнейшая, универсальная связь между эволюционными и молекулярно-фенотипическими переменными состоит в отрицательной корреляции скорости эволюции белок-кодирующих генов и уровня экспрессии: высокоэкспрессированные гены эволюционируют медленно. Эта зависимость наблюдается у всех организмов, для которых есть данные по экспрессии генов (Drummond et al., 2006; Drummond and Wilke, 2008; Pal et al., 2001). Поскольку, как отмечено выше, существует положительная корреляция между Ка и Ks, неудивительно, что скорости эволюции синонимических и несинонимических сайтов связаны с уровнем экспрессии гена качественно одним и тем же образом. Более неожиданно то, что зависимость между экспрессией и скоростью эволюции соблюдается и для 3’-нетранслируемого участка (НТУ), хотя и не обнаружена для 5’-НТУ (Jordan et al., 2004). Эта универсальная отрицательная корреляция проявляется еще сильнее, если сравнивать скорость эволюции напрямую с экспериментально измеренными концентрациями белка (Schrimpf et al., 2009).

Открытие универсальной связи между экспрессией генов и их эволюцией стимулировало смелую попытку новой интерпретации, согласно которой эволюция белков определяется в большей степени принципами структуры и укладки белка, общими для всех организмов, чем его уникальными биологическими функциями. Было выдвинуто предположение, впервые — в работе Алана Драмонда и Клауса Вилке, о том, что главным фактором отбора в эволюции белка является его устойчивость к неправильной укладке. Согласно этой гипотезе, влияние мутации, как геномной, так и фенотипической (вызванной ошибками трансляции), на приспособленность организма в первую очередь рассматривается как следствие отрицательного эффекта от неправильной укладки белка, которая, помимо вызываемых ею энергетических издержек, может быть еще и токсичной для клетки (Drummond et al., 2005; Drummond and Wilke, 2008). Не углубляясь в детали, заметим, что эта интуитивно привлекательная модель может естественным образом объяснить отрицательную корреляцию между экспрессией генов и эволюцией генных последовательностей: очевидно, что негативный эффект от неправильной укладки должен быть выше для высокоэкспрессированных белков, чем для белков, производимых в небольших количествах. Другими словами, уровень экспрессии — это линза, которая увеличивает любое негативное влияние на приспособленность, связанное с данной последовательностью белков, и важнейшее из таких влияний обусловлено неправильной укладкой белка. Таким образом, гены высокоэкспрессируемых белков подвергаются бо?льшим ограничениям, следствием чего является низкая скорость их эволюции. Эта гипотеза совместима с твердо установленным принципом предпочтительного выбора кодона (среди синонимичных кодонов чаще встречается оптимальный)[37] в высокоэкспрессируемых и высококонсервативных белок-кодирующих генах, а также с положительной корреляцией между Ka и Ks. Согласно гипотезе эволюции, движимой ошибками укладки, эволюция синонимичных сайтов ограничена, по крайней мере частично, теми же самыми факторами, что и эволюция последовательности белка, поскольку выбор оптимального кодона, обеспечивающий более быструю и точную трансляцию, особенно важен для высокоэкспрессированных белков и для тех конкретных позиций, которые влияют на укладку белка. Таким же образом можно объяснить и эволюцию 3-НТУ — этот нетранслируемый участок используется для регуляции процесса трансляции.

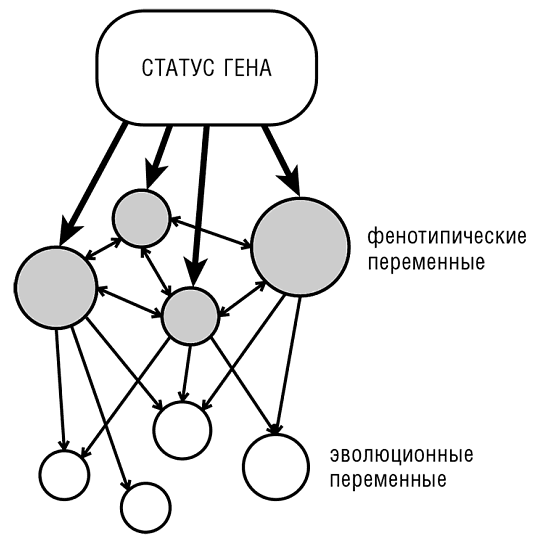
Рис. 4-4. Модель «статуса генов».

В работе, выполненной совместно с Александром Лобковским и Юрием Вульфом, мы задались вопросом, не удастся ли в данном случае убить двух зайцев, то есть возможно ли объяснить эволюцию белок-кодирующих генов и практически повсеместную отрицательную корреляцию между эволюционными скоростями и уровнем экспрессии в рамках одной простой модели (Lobkovsky et al., 2010). В анализе эволюции, ведомой ошибками укладки, проводимом для «безрешеточной»[38] модели укладки белка, были получены оценки эволюционных скоростей для гипотетического случая, в котором ошибки укладки белка являются единственным фактором, влияющим на приспособленность организма. Результаты анализа воспроизвели, и весьма точно, универсальное распределение эволюционных скоростей белков, а также зависимость между скоростью эволюции и экспрессией. Этот результат позволяет предположить, что универсальный закон распределения скоростей эволюции и в самом деле вытекает из фундаментальных физических принципов укладки белка.

Слабость или даже отсутствие некоторых интуитивно ожидаемых корреляций между эволюционными и фенотипическими переменными кажутся не менее поразительными, чем обнаруженные корреляции. В самом деле, биологическая интуиция всей этой области знаний подсказывает, как было указано в начале этого раздела, что гены с большей «биологической значимостью» будут эволюционировать медленнее и будут теряться с меньшей вероятностью (Wilson et al., 1977). Общее понятие биологической важности можно конкретизировать измерением фенотипических эффектов от нокаута или других мутаций многих генов — желательно всех генов многих организмов. Можно предположить, что чем больше эффект от нокаута гена, тем медленнее этот ген будет эволюционировать, и гены, утрата которых вызывает летальный эффект, будут эволюционировать значительно медленнее генов, менее существенных для выживания. К настоящему времени проведено сравнение фенотипических эффектов нокаута генов и скоростей эволюционирования генов для множества модельных организмов и получен недвусмысленный и как будто парадоксальный результат: связь между экспериментально измеренной биологической важностью гена и скоростью его эволюции очень слаба, если вообще существует (Hurst and Smith, 1999; Jordan et al., 2002; Krylov et al., 2003; Wang and Zhang, 2009). Еще более удивительным кажется отсутствие сильной корреляции между скоростью утраты гена в течение эволюции, представляющей в некотором смысле временную меру биологической важности или существенности гена, и экспериментально определенным эффектом на приспособленность: только те наборы генов, которые вообще не утрачиваются на продолжительных отрезках эволюции, таких как вся эволюция эукариот, обогащены «важными» генами (Krylov et al., 2003; Wang and Zhang, 2009). Первые работы, показавшие почти полное отсутствие связи между скоростью эволюции и биологической значимостью, были основаны на простом измерении эффекта (присутствует/отсутствует) нокаута гена (соответственно, существенный/несущественный ген). Можно предполагать, что такие измерения слишком грубы и не дают осмысленной оценки биологической важности. Однако, например, в последних работах лаборатории Джорджа Занга было продемонстрировано почти полное отсутствие корреляции между скоростью эволюции и весьма точно измеренным влиянием на приспособленность пекарских дрожжей (S. cerevisiae) во множестве различных условий (Wang and Zhang, 2009), что уменьшает вероятность получения неадекватных результатов.

Чем же тогда объяснить неожиданно слабую связь между эволюцией и функцией гена? По отношению к эволюции последовательностей можно предположить, что скорость эволюции более зависит от внутренних характеристик гена (в особенности от структуры кодируемого белка), чем от его биологической значимости. Однако это объяснение неприменимо к случаям утраты гена. Наиболее осмысленным — хотя опять-таки противоречащим здравому смыслу — кажется следующее объяснение: фенотипический эффект нокаута гена (и в целом — набора необходимых генов) не проявляется как консервативное свойство в эволюционном процессе и быстро меняется (в масштабах эволюционной шкалы), вероятно благодаря высокой скорости эволюции сетей взаимодействующих генов[39]. Ясно, что это предположение можно проверить опытным путем, пусть и с помощью трудоемких экспериментов.

Почти нейтральные сети и белковая эволюция

В целом скорость эволюции гена определяется размером его почти нейтральной сети, то есть множества последовательностей, получаемых друг из друга в результате одношаговых мутаций (пусть и необязательно с помощью одной замены) и имеющих приспособленность примерно такую же, как и у наиболее приспособленной последовательности (Wagner, 2008a; Wolf et al., 2010). Чем больше нейтральная сеть, тем слабее ограничения для конкретного гена, тем быстрее он может эволюционировать (рис. 4-5).

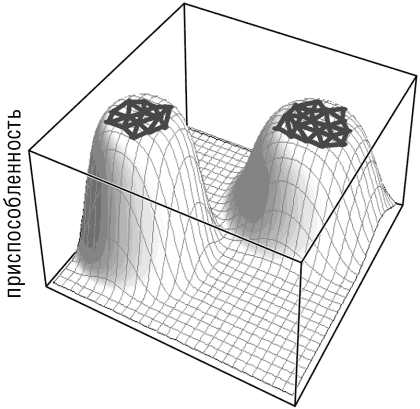
Рис. 4-5. Почти нейтральная сеть и белковая эволюция. Две почти нейтральные сети для двух вымышленных белков схематично представлены как две области, находящиеся на широких вершинах пиков приспособленности.

В эволюции белка приспособленность отдельной последовательности в основном зависит от ее устойчивости к ошибкам укладки и от уровня экспрессии, а размер почти нейтральной сети зависит от высоты и формы пика, занимаемого этой последовательностью и ее соседями на ландшафте устойчивости (рис. 4-6). В этой модели высокоэкспрессированные белки, чьи исходные последовательности высоко устойчивы к ошибкам укладки, занимают высокие и крутые пики с небольшой областью высокой приспособленности (малые почти нейтральные сети) и, следовательно, подвержены сильному стабилизирующему отбору и медленно эволюционируют. И наоборот, белки с более низким уровнем экспрессии и меньшей устойчивостью находятся на более низких, пологих пиках, имеют более широкую область высокой приспособленности и, соответственно, подвержены более слабому отбору и имеют высокую скорость эволюции (рис. 4-6; Wolf et al., 2010).

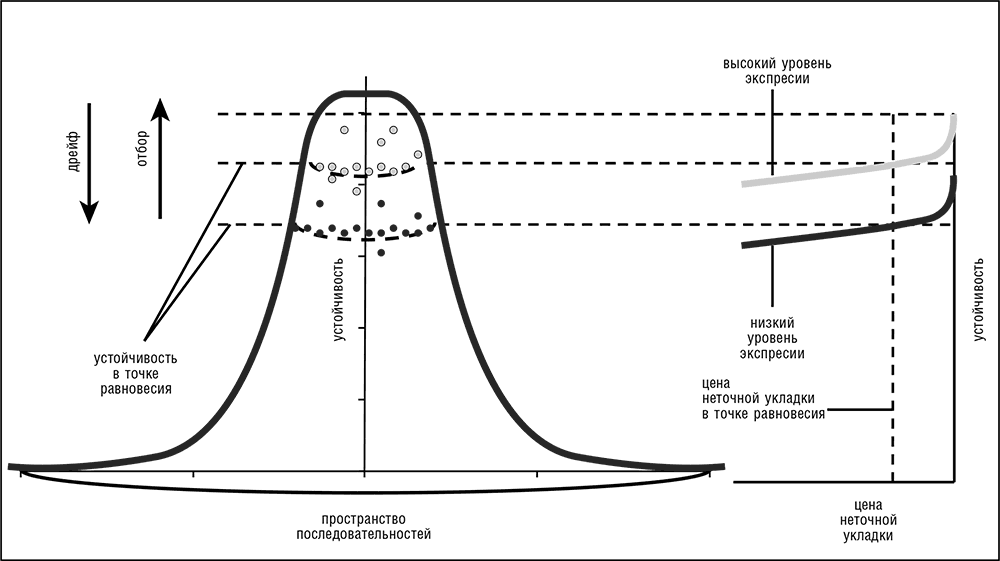
Рис. 4-6. Модель эволюции белка, управляемой издержками неточной укладки.

Геномная эволюция путем дупликации генов, модель рождения и смерти гена и универсальное распределение численности паралогичных семейств

Мы уже касались вопроса дупликации генов в предыдущей главе, в частности при построении списка важнейших механизмов геномной эволюции. Однако есть еще по крайней мере два хороших повода вернуться к этому механизму эволюции и обсудить его более детально. Во-первых, дупликация несомненно является одним из главных путей геномной эволюции для всех форм жизни и играет принципиальную роль в эволюции эукариот (см. гл. 8). Во-вторых, эволюция путем дупликации генов представляет собой формально простой процесс, для которого довольно легко построить хорошо работающие физические (или математические) модели, которые и рассматриваются в этой главе.

Представление о дупликации как об исключительно эффективном способе геномной эволюции лежит в основе современного эволюционного мышления. Упрощенно говоря, сущность этого представления состоит в том, что создание новых функциональных объектов (белков и РНК) путем модификации уже имеющихся (вспомните модель «эволюции как мастерового» Жакоба; Jacob, 1977) — это, очевидно, намного более простой путь, чем создание этих объектов с самого начала, с нуля (история этой идеи рассказывается в гл. 2). Как и другие представления геномики, эволюция путем генной дупликации имеет строгие количественные подтверждения — большинство генов в геноме принадлежат семействам паралогов (за исключением очень небольших геномов, таких как у микоплазмы и других паразитических бактерий; Jordan et al., 2001). Более детальная реконструкция эволюции показывает, что дупликация проявляется, с различной интенсивностью, на всех этапах эволюции, таким образом, любой геном — это набор дупликаций самого различного возраста. Выбирая некоторую эволюционную линию, допустим, животные — хордовые — млекопитающие — приматы — и т. д., мы можем обнаружить в геноме (например, в нашем) все соответствующие классы дупликаций: дупликации, специфичные для животных, дупликации, специфичные для хордовых, специфичные для приматов и т. д. (Lespinet et al., 2002).

Распределение численности паралогичных семейств в любом геноме — еще одна универсальная статистическая закономерность, обнаруженная сравнительной геномикой (рис. 4-7). Распределения для всех геномов приблизительно описываются степенной функцией с отрицательным показателем степени: y = ax–? (где ? — положительное число, a — коэффициент; Koonin et al., 2002; Luscombe et al., 2002). Эти распределения, имеющие в двойных логарифмических координатах вид прямых линий, показывают, что большинство семейств по численности малы (включая семейства геномов с преобладанием синглетонных сайтов), и только немногие семейства включают в себя большое число паралогов.

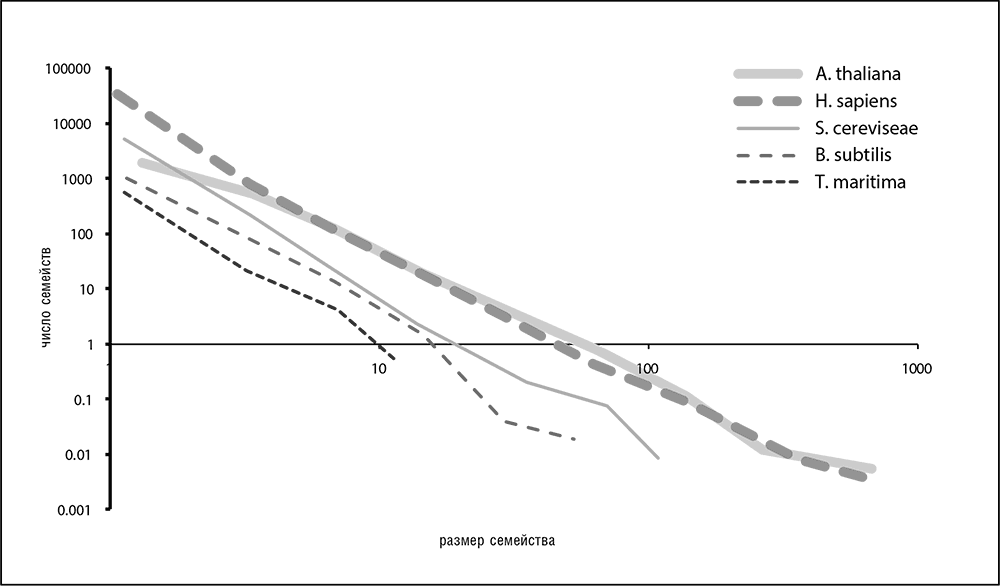
Рис. 4-7. Распределение размера семейств паралогичных генов для нескольких сильно отличающихся геномов. Показаны распределения для растения резуховидки Таля (A. thaliana), человека (H. sapiens), для пекарских дрожжей (S. cereviseae), для сенной палочки (B. subtilis) и для бактерии Thermotoga maritima. Использованы данные из базы данных EggNog (Jensen et al., 2008)

Возникновение универсальной степенной закономерности распределения численности паралогичных семейств может быть описано с высокой точностью простой математической моделью эволюционного процесса (рис. 4-8). Эта модель основана на математической теории так называемых процессов рождения и смерти (один из видов марковских процессов) и для случая эволюции путем генной дупликации чаще называется моделью рождения, смерти и инновации (Karev et al., 2002). В рамках этой модели рождение — это такая генная дупликация, при которой появляется новый член паралогичного семейства, смерть — утрата гена, а инновация — это рождение нового семейства либо путем такой дупликации, которая вызывает быструю эволюции и тем самым как бы стирает «память» старого семейства, либо путем горизонтального переноса генов[40]. Наиболее интересный результат этого моделирования состоит в том, что эта модель эволюции путем генной дупликации воспроизводит рассмотренные нами распределения численности семейств паралогичных генов только при соблюдении вполне определенных условий: частоты рождения и смерти гена должны быть примерно равными и зависеть от численности семейства таким образом, чтобы большие семейства оказывались более динамичными, чем маленькие.

Стоит подчеркнуть, что динамика эволюции генного семейства описывается именно той стохастической моделью, которая используется в статистической физике. Однако, чтобы эта модель была совместима с полученными данными, необходимо соблюдение тонкого баланса между рождением, смертью и обновлением, и похоже, что этот баланс поддерживается естественным отбором. Примечательно, что эта и подобные модели описывают с одинаковой точностью эволюцию геномов как прокариот, так и эукариот, несмотря на существенные различия между процессами, ведущими к образованию семейств паралогичных генов. Для эукариот важнейшим, если не единственным, процессом, лежащим в основе эволюции семейств, является «честная» генная дупликация, a для прокариот количественно более важным является горизонтальный перенос генов (поэтому такие генные семейства «псевдопаралогичны»; см. гл. 5 и 7). Тот факт, что рассмотренные здесь модели одинаково хорошо описывают биологически отличающиеся процессы эволюции генома, ведущие к сходным результатам, с одной стороны, подчеркивает универсальность этих моделей, а с другой — указывает на их ограниченную ценность для биолога.

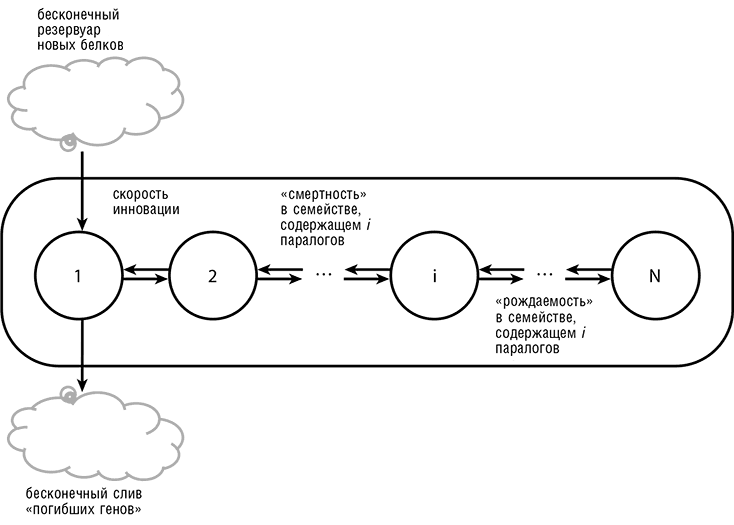
Рис. 4-8. Модель рождения, смерти и инновации в применении к эволюции генных семейств. Под рождением подразумевается генная дупликация или приобретение псевдопаралогичного гена путем горизонтального переноса с последующим расширением паралогичного семейства, смертью называется утрата гена (независимо от способа утраты), а инновацией считается приобретение нового гена, который становится родоначальником нового семейства (Karev et al., 2002)

Структура и эволюция сетей: всеобщность степенного закона и стоящие за ним фундаментальные процессы

Сеть (network) — популярнейшее понятие системной биологии, повсеместно пронизывающее современную культуру, не только в рамках биологии или науки в целом[41]. В самом деле, трудно придумать более естественный способ представления связей между многочисленными объектами, чем сеть (в математике рассматриваемую как ориентированный или неориентированный граф). В биологическом контексте узлами (или иначе — вершинами) сети часто представляют гены или белки, а ребрами (связями между узлами) обозначают их взаимодействия, которые могут быть физическими, генетическими или регуляторными (Barabasi and Oltvai, 2004). К настоящему времени разработано множество методов описания и сравнения структур (топологий) сетей (табл. 4-1). Наиболее часто для анализа используется понятие функции распределения степеней вершин, где под степенью вершины понимают число ребер, связывающих эту вершину с другими. Сравнение таких функций, выполненное для сетей различного типа, показало принципиальное отличие биологических сетей (а также многих небиологических, включая Интернет) от случайных графов: случайные графы имеют колоколообразное распределение Пуассона, а для биологических сетей распределения описываются степенной функцией (табл. 4-1). Сети, имеющие степенные функции распределения степеней вершин, называют масштабно-инвариантными сетями, так как графики их функций внешне не меняются при масштабировании (обратите внимание на прямую линию в двойных логарифмических координатах на табл. 4-1). Такие сети всегда содержат небольшое число вершин с высокими степенями, так называемых хабов (hubs), и большое число слабосвязанных вершин.

Таблица 4-1

Случайные и масштабно-инвариантные сети

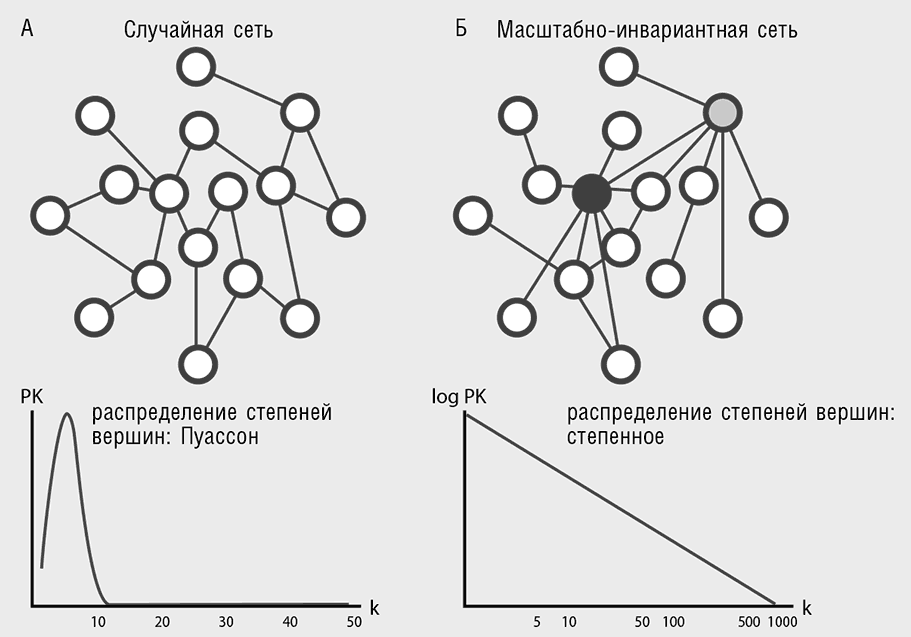
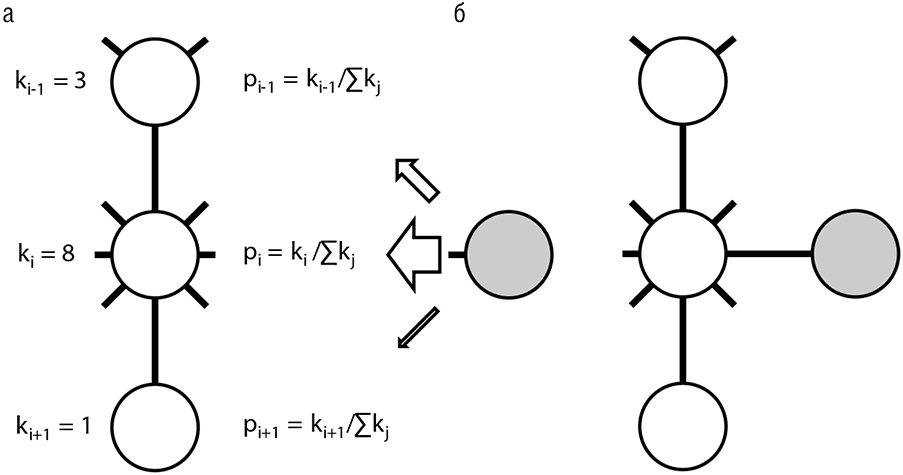
Рис. 4-9. Предпочтительное присоединение в эволюции биологических сетей: а — фрагмент сети и новый добавляемый элемент; б — результат включения новой вершины в сеть. ki = степень i-й вершины, pi = вероятность присоединения новой вершины к вершине i (см. табл. 4-1)

Примечательно, что степенная функция распределения степеней вершин, по всей видимости, является неотъемлемым свойством эволюционирующих сетей (включая Интернет) и не обязательно имеет биологическое происхождение. Все типы биологических сетей, как описывающих физические взаимодействия между белками, так и отражающих взаимную регуляцию генов, несомненно, появились в результате эволюции и обладают указанным типом распределения (другими словами, являются масштабно-инвариантными). Для объяснения универсального степенного закона распределения Барабаши с коллегами предложили принцип предпочтительного присоединения (preferential attachment) новых вершин, что на простом циничном языке означает, что в процессе эволюции сети «богатые делаются еще богаче» (Barabasi, 2002). Предпочтительное присоединение представляет собой стохастический, неадаптивный процесс. В самом деле, когда создается новый сайт в Интернете и случайно связывается с другими сайтами, с большей вероятностью он окажется связанным с хабом, чем с изолированным сайтом, просто потому что очень многие различные пути в сети ведут к хабам (табл. 4-1). Этот режим эволюции по своей природе консервативен — сеть сохраняет свою структуру в процессе роста. Является ли предпочтительное присоединение главным принципом эволюции биологических сетей? По этому вопросу еще не достигнуто согласия. В случае если этот принцип существен для биологических сетей, должны обнаружиться некоторые специфические биологические механизмы, обеспечивающие его выполнение (рис. 4-9). Высокая интерактивность хабов, представленная «липкостью» некоторых белков, склонных к взаимодействиям, не обязательно функционально значимым, со многими другими белками, могла бы быть одним из таких механизмов. Еще более важный вклад в формирование сетей осуществляется посредством важнейшего механизма эволюции — генной дупликации. Когда ген удваивается, все имеющиеся его связи с другими генами также удваиваются, а потом начинают постепенно расходиться в процессе последующей эволюции. В простейшей модели эволюции (такой как сбалансированная модель рождения, смерти и обновления), если частота генной дупликации пропорциональна размеру семейства, структура сети (то есть распределение степеней вершин) будет сохраняться даже при отсутствии давления отбора (Koonin et al., 2002; Lynch, 2007a).

Разбиение генома по биологическим функциям: универсальный степенной закон

До сих пор в нашем обсуждении универсальных количественных закономерностей в геномной эволюции мы преднамеренно обходили стороной вопрос биологических функций. Конечно, это абстракция: геном ни в коем случае не сумма безликих «молекул», а ансамбль генов, каждый из которых кодирует определенную биологическую функцию[42]. Сначала может показаться неожиданным, что способ рассуждения, позаимствованный из статистической физики, может быть применен и к биологическим функциям. Для применения такого подхода необходимо разделить гены на большие функциональные классы, о которых можно думать как о разных типах «молекул» и которые пригодны для статистического анализа, если они включают достаточно много генов.

Как показывается в серии доскональных исследований Эрика Ван Нимвегена[43], различные функциональные классы генов по-разному соотносятся с общим числом генов в геноме (Molina and van Nimwegen, 2009; van Nimwegen, 2003). Не учитывая некоторые отклонения, для прокариот можно указать три основных показателя степени, описывающие эти соотношения: 0, 1 и 2. Генам белков, участвующих в информационных процессах (трансляции, транскрипции и репликации), соответствует показатель степени 0 — число таких генов достигает некоторого константного значения уже в минимальных геномах и в принципе не зависит от сложности генома. Число метаболических ферментов и транспортных белков примерно прямо пропорционально общему числу генов (показатель степени 1). Регуляторные гены и компоненты систем передачи сигналов показывают квадратичную зависимость (показатель степени равен 2; рис. 4-10). Показатели степени этих трех обширных классов остаются неизменными, с очень небольшими отклонениями, для всех групп прокариот, и это позволяет предположить, что разница в эволюционной динамике генов с различными функциями отражает какие-то фундаментальные законы эволюции клеточных организмов, или, другими словами, строгие и четко выраженные ограничения в функциональном устройстве геномов. Для генов эукариот обнаружены похожие, хотя и не такие явные, степенные соотношения, показатель степени для регуляторных генов эукариот значительно больше 1 (хотя и меньше 2). Имея в виду все вышесказанное, можно заключить, что эти соотношения представляют еще один набор универсалий геномной эволюции, которые становятся еще интереснее при рассмотрении их связи с функциональным устройством клетки.

Фундаментальные причины существования различных соотношений для различных функциональных классов генов еще не выяснены. Привлекательно простая модель эволюции метаболических сетей прокариот как «ящика с инструментами», предложенная Сергеем Масловым и коллегами, может быть первым шагом на пути объяснения квадратичной зависимости, характерной для регуляторных генов (Maslov et al., 2009). В этой модели ферменты, необходимые для утилизации новых метаболитов, добавляются вместе с соответствующими им регуляторами (в первую очередь посредством горизонтального переноса генов, гл. 5) во все более развитую сеть реакций. В результате усложнения сети, обеспечивающей все большее разнообразие ферментов промежуточных реакций, увеличивается отношение числа регуляторных генов к регулируемым. В какой-то момент, и его наступление можно точно предсказать, цена добавления новых регуляторов неизбежно станет слишком невыгодной («разрастающаяся бюрократия») и будет ограничивать рост сложности генома.

Гипотеза «бюрократического потолка» для верхней границы сложности генома выглядит особенно правдоподобно в свете почти полного отсутствия роста числа генов в геномах позвоночных, особенно млекопитающих (и в наших геномах тоже), для которых связь между числом генов и размером генома очевидно нарушена (см. гл. 3 и 8). В принципе число генов могло бы быть напрямую ограничено ценой репликации ДНК, но для огромных геномов позвоночных этот фактор можно смело исключить как главное ограничение. Соответственно, цена регуляции, возможно совместно с ценой экспрессии, выглядит наиболее вероятным кандидатом на роль основного фактора, ограничивающего рост числа генов. Поэтому не случайно позвоночные (и в меньшей степени другие многоклеточные эукариоты) выработали новые, замысловатые способы увеличения сложности протеома, такие как широко распространенный альтернативный сплайсинг, альтернативная трансляция и сложная регуляция (в особенности обширный, все еще слабо изученный набор регуляторных РНК). Такие формы сложности не вызывают инфляционный рост числа белок-кодирующих генов и, таким образом, снижают по крайней мере некоторые издержки, особенно издержки трансляции (см. гл. 8).

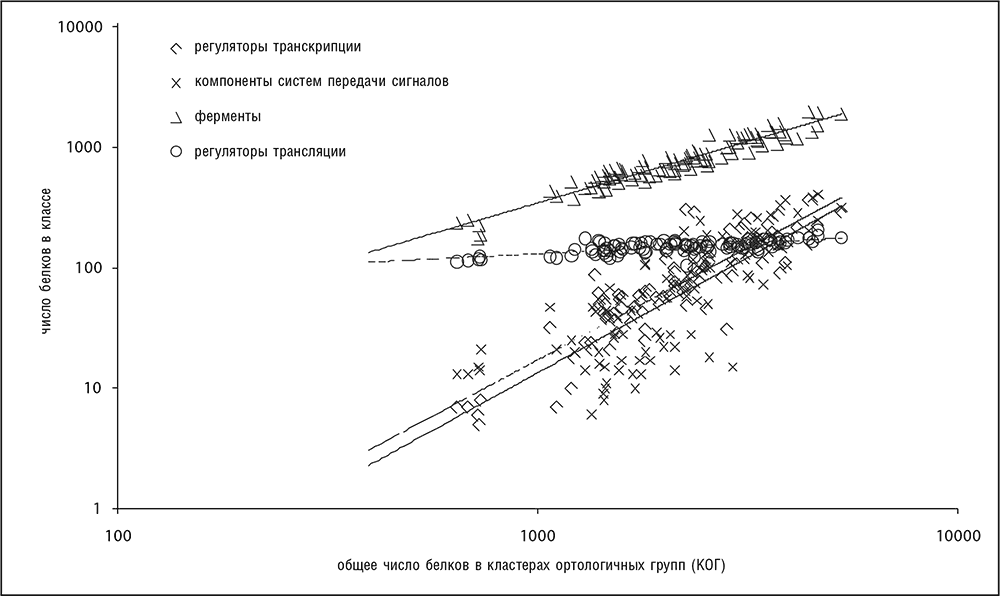
Рис. 4-10. Четко различающиеся соотношения между различными функциональными классами генов и размером генома (общим числом белок-кодирующих генов) прокариот. Использована информация из базы данных COG (Tatusov et al., 2003). График построен в двойных логарифмических координатах.

Универсальная зависимость численности функциональных классов генов от размера генома находится в обратной зависимости с ранее описанным степенным законом распределения численности семейств генов. Чем больше положительный показатель степени функции зависимости от размера генома для функционального класса генов (рис. 4-10), тем меньше отрицательный показатель степени функции распределения численности семейств в этом классе (рис. 4-7). Кажется интуитивно правдоподобным, что функциональные классы с сильной зависимостью от размера генома должны содержать много больших семейств паралогичных генов. Обратная зависимость этих двух универсалий генома была выведена в рамках простой эволюционной модели, в которой используются правила пропорциональных вычислений для функциональной композиции генома, например «добавить два регулятора на каждый метаболический фермент» (Grilli et al., 2011). Предсказания этой модели подтверждаются эмпирическими данными для многих геномов бактерий и архей.

Стохастичность, нейтральность и отбор в эволюции

В предыдущих разделах этой главы мы ознакомились со многими количественными универсалиями, отражающими важнейшие аспекты эволюции и функционирования генома. Среди этих универсалий мы рассматривали вездесущий степенной закон распределения, который описывает как структуру всех биологических сетей, так и семейства паралогичных генов в разнообразных геномах, близкое к логарифмически нормальному распределение скоростей эволюции генов и универсальные корреляции, такие как отрицательная корреляция между генной экспрессией и скоростью эволюции. Какова природа этих универсалий? Отражают ли они какие-то глубокие свойства эволюции или это просто статистические эффекты, не имеющие отношения к пониманию биологических явлений? Здесь и далее в этой книге (гл. 13) будет отстаиваться точка зрения на эти универсалии как на нетривиальные, характерные и биологически значимые тенденции, хотя они отражают только одну из двух (а возможно, и большего числа) дополнительных (в смысле принципа дополнительности Бора) составляющих эволюции жизни[44].

Во-первых, как это уже отмечалось и теперь совершенно очевидно, все эти универсалии зависимы от поведения совокупностей генов, фундаментальных единиц эволюции, рассматриваемых как статистические ансамбли. Таким образом, эти универсальные зависимости и распределения являются эмергентными свойствами биологических систем, то есть свойствами, проявляющимися в результате того, что эти системы состоят из многочисленных (достаточно многочисленных для проявления устойчивых статистических закономерностей) элементов (генов или белков, в зависимости от контекста), слабо взаимодействующих друг с другом (если сравнивать эти взаимодействия с теми, которые поддерживают целостность самих этих элементов).

Во-вторых, как мы уже видели, современный эволюционный анализ не останавливается на демонстрации существования универсальных понятий и законов. По крайней мере некоторые ключевые универсалии, такие как распределение эволюционных скоростей, отрицательные корреляции между скоростью эволюции и экспрессией и распределение численности паралогичных семейств, были теоретически выведены в рамках простых, но достаточно детализированных, формальных моделей эволюции. Способность простых моделей, в которых в качестве элементарных событий рассматриваются наиболее общие эволюционные процессы (такие как дупликация и утрата генов), объяснять геномные универсалии убеждает в том, что эти универсалии отражают существенные черты эволюции.

Третье, и, возможно, наиболее важное, замечание о новой парадигме понимания эволюции, которую мы пытаемся здесь обрисовать, состоит в том, что порождающие модели для общегеномных универсалий либо совсем не используют понятие отбора, либо используют только понятие очищающего (стабилизирующего) отбора. Эта форма отбора направлена на сохранение статуса-кво и наблюдается для укладки белковых молекул, для распределения численности генных семейств и для универсальной зависимости численности функциональных классов генов от общего числа генов (Koonin and Wolf, 2010b).

Аналогия между эволюционным процессом и статистической физикой не ограничена существованием универсальных зависимостей и распределений, некоторые из которых могут быть выведены в рамках простых моделей. Возможно также составить схему детального соответствия ключевых параметров этих двух областей (Barton and Coe, 2009; Sella and Hirsh, 2005). Такой параметр состояния (степень свободы), как положение частицы, в этой схеме является аналогом либо состояния сайта в нуклеотидной или белковой последовательности, либо состояния гена в геноме (в зависимости от уровня моделирования эволюции), и тогда параметрам скорости эволюции для сайта или гена будет соответствовать скорость частицы. Более того, значение эффективной численности популяции будет очевидно аналогичным значению температуры в статистической физике, а приспособленность будет соответствовать свободной энергии.

Краткий обзор и перспектива: о природе эволюционного процесса

Результаты взаимопроникновения сравнительной геномики и системной биологии, обсуждаемые в данной главе, приводят нас к следующему ключевому обобщению.

Многие, чтобы не сказать все, общие закономерности геномной и молекулярно-фенотипической эволюций описываются стохастическими процессами, основанными на принципе подверженной ошибкам репликации и ограниченными очищающим отбором, который поддерживает существующую общую (но не специфическую) архитектуру генома и устройства клеток.

Это обобщение не следует понимать как исключение адаптации из числа важнейших эволюционных понятий. Разумеется, адаптация — это общее и неотъемлемое явление в эволюции всех форм жизни. Тем не менее становится все более ясным, что общие количественные характеристики геномной архитектуры, функционирования и эволюции в первую очередь определяются неадаптивными, стохастическими процессами. Адаптация только модулирует эти закономерности. Здесь становится очень соблазнительным провести вполне очевидную параллель с нейтральной теорией Кимуры. В ходе высокоуровневого анализа геномных и молекулярно-фенотипических параметров мы начинаем различать контуры «неонейтрализма» (см. также гл. 8).

Аналогия между эволюцией и стохастическими физическими процессами ни в коем случае не отрицает метафоры «эволюции как мастерового» Жакоба. Напротив, новые открытия в эволюционной геномике прекрасно вписываются в это представление об эволюции: естественный отбор (адаптивный компонент эволюции) представляет собой процесс «латания», не полную перестройку или создание нового объекта, а добавление к существующему новых частей из уже имеющихся подручных материалов. Таким образом, первичная форма отбора — это очищающий отбор, который поддерживает статус-кво. Это обобщение имеет довольно удивительное, но неизбежное следствие: большая часть наиболее значимых событий во всей истории жизни произошла в течение первых нескольких сотен миллионов лет существования жизни на Земле, до появления современного типа клеток. Этот период в истории жизни должен был качественно отличаться от всей остальной эволюции; есть основания считать, что важнейшее достижение эволюции — это появление клетки, все остальное уже не так важно. Мы будем обсуждать происхождение жизни с этой точки зрения в главах 11 и 12 и вернемся к обсуждению общей природы эволюции в главе 13.

Параллели между эволюционной биологией и статистической физикой оказались точными и фундаментальными до такой степени, что кажется вполне справедливым заключение о том, что это не аналогии, а проявление общих статистических принципов (если не сказать законов) поведения больших ансамблей слабовзаимодействующих объектов[45]. Как в физике, так и в эволюционной биологии такие ансамбли (например, идеальный газ в физике и геном как сумма генов в биологии) являются идеализациями. В реальности отклонения от поведения, которое предсказывается простыми статистическими моделями, неизбежны и значимы. В эволюционной биологии такие отклонения, кроме всего прочего, вызываются различными взаимодействиями генов, что приводит к неожиданным эффектам, таким как отсутствие строгой корреляции между биологической значимостью гена и скоростью его эволюции. Тем не менее существенный эвристический потенциал прямого статистического подхода в объяснении по крайней мере некоторых фундаментальных свойств как физических, так и биологических процессов неоспорим.

Рекомендуемая дополнительная литература[46]

Barabasi, A. L., and Z. N. Oltvai. (2004) Network Biology: Understanding the Cell’s Functional Organization. Nature Reviews Genetics 5: 101–113.

Обзор свойств биологических сетей с акцентом на масштабной инвариантности.

Barton, N. H., and J. B. Coe. (2009) On the Application of Statistical Physics to Evolutionary Biology. Journal of Theoretical Biology 259: 317–324.

Технически сложная, но важная работа по термодинамическому подходу в эволюционной биологии.

Drummond, D. A., and C. O. Wilke. (2009) The Evolutionary Consequences of Erroneous Protein Synthesis. Nature Reviews Genetics 10: 715–724.

Критический обзор концепции эволюции, ограниченной ошибками трансляции и ошибками укладки белка.

Lobkovsky, A. E., Y. I. Wolf, and E. V. Koonin. (2010) Universal Distribution of Protein Evolution Rates As a Consequence of Protein Folding Physics. Proceedings of the National Academy of Sciences USA 107: 2,983—2,988.

В этой работе эволюционная динамика выводится в рамках простой модели укладки белка и с хорошей точностью воспроизводится универсальное распределение эволюционных скоростей.

Koonin, E. V., and Y. I. Wolf. (2006) Evolutionary Systems Biology: Links Between Gene Evolution and Function. Current Opinion in Biotechnology 17: 481–487.

Обзор корреляций между эволюционными и молекулярно-фенотипическими параметрами.

Koonin, E. V., Y. I. Wolf, and G. P. Karev. (2002) The Structure of the Protein Universe and Genome Evolution. Nature 420: 218–223.

Обсуждение универсальных распределений и зависимостей с акцентом на роли стохастических процессов и принципе предпочтительного присоединения.

Molina, N., and E. van Nimwegen. (2009) Scaling Laws in Functional Genome Content Across Prokaryotic Clades and Lifestyles. Trends in Genetics 25: 243–247.

Последние данные по универсальным степенным функциям для различных функциональных классов генов.

Sella, G., and A. E. Hirsh. (2005) The Application of Statistical Physics to Evolutionary Biology. Proceedings of the National Academy of Sciences USA 102: 9,541—9,546.

Богатая идеями статья, детально описывающая формальную аналогию между статистической физикой и эволюционной динамикой.

Данный текст является ознакомительным фрагментом.