Глава 29 Применение математики и кибернетики в биологии
Процесс проникновения математики в биологию имеет длительную историю. Однако сильнее всего он проявился в XX в. и главным образом в последние 20–25 лет. Это прежде всего связано с развитием самой биологии, ее теоретических представлений. Системы биологических понятий достигли той степени абстрактности и точности, при которой стало возможным использование математических моделей для описания биологических явлений. Кроме того, структура изучаемых в настоящее время биологических систем оказалась столь сложной, что потребовала для своего анализа разработки новых принципов исследования, основанных на точных математических методах.
Важную роль в математизации биологии сыграло взаимопроникновение наук. Биология издавна испытывала влияние представлений, возникавших в механике и физике. Достаточно вспомнить попытки сравнения скелета позвоночных с системой рычажных механизмов (Леонардо да Винчи, Дж. Борелли). Возникшая из этих попыток биомеханика начала особенно интенсивно развиваться в первой четверти XX в. (Я.И. Грдина, Н.А. Бернштейн и др.). Сближение биологической тематики с физическими и химическими проблемами является одним из путей проникновения в биологию математики, давно играющей важную роль в физике и химии.
Большое значение имели также некоторые идеи, возникшие вне биологии и проникшие в нее в последние десятилетия. Это главным образом идеи теории регулирования и теории информации. Они привели к тому, что существенно изменился подход к регуляторным системам организма, к работе рецепторов и т. д. Понятия «обратной связи», «информации», органически связанные с математическими представлениями, явились существенным каналом проникновения математики в биологию.
Как известно, в последние десятилетия в математике возник ряд новых направлений, связанных с изучением моделей систем высокой степени сложности. К ним относятся теория автоматов, теория игр, теория операций и др. В этой связи биология оказалась для математиков интересным объектом, на котором можно проверить силу новых теорий при помощи вновь созданных математических дисциплин и вычислительных машин.
Более того, источником новых математических идей стала сама биология, Некоторые примеры такого рода могут быть отмечены даже в биологии XIX в. Так, Г. Гельмгольц исследовал некоторые уравнения математической физики в связи со своими работами по физиологии слуха. Известно, что некоторые работы Р. Фишера по математической статистике были связаны с его занятиями биологией. Работы В. Вольтерры по интегральным уравнениям базировались на его исследованиях в области экологии.
Однако именно в настоящее время биология оказывается особенно привлекательной для математика. Сложность таких явлений, как работа мозга, взаимосвязи в биологических сообществах, высокая способность организмов к адаптации, размножению и т. д. привели к выводу, что для их описания потребуется создание новых математических конструкций. Так размышления о математических моделях размножения привели, например, Дж. Неймана к созданию теории самовоспроизводящихся автоматов. Именно биология как источник новых моделей, как наука, изучающая объекты, не имеющие аналогов в физике и технике, и потому позволяющая ставить совершенно новые задачи, привлекла к себе внимание таких математиков, как Р. Беллман, Н. Винер, Г. Вейль, И.М. Гельфанд (Ленинская премия, 1955), А.Н. Колмогоров (Ленинская премия, 1965), А.А. Ляпунов, Дж. Нейман и др.
Некоторые закономерности проникновения математических методов и идей в биологию.
На раннем этапе математика проникала в биологию через посредство смежных наук, прежде всего через механику и физику. При этом случаи применения математических методов носили эпизодический характер. Наиболее известные примеры такого рода дают работы Дж. Борелли (1680–1681) о движении животных, Л. Эйлера (1730), Ж. Пуазейля (1840) и Дж. Стокса (1845) по гемодинамике и Г. Гельмгольца по физиологической оптике (1867) и акустике (1863). При этом биологическая проблема формулировалась как одна из задач механики или физики. Начиная с первой трети XX в. математика получает в биологии систематическое применение для решения собственно биологических проблем и эти науки начинают обходиться без посредников.
Вторая закономерность проникновения математики в биологию связана с изменением способа применения математики. Первоначально систематическое использование математики определялось развитием методов обработки результатов эксперимента, прежде всего, методов математической статистики. На базе использования этих методов возникла специальная наука — биометрия. Кроме того, математика использовалась для сокращенного описания результатов экспериментов, для выявления эмпирических функциональных связей и подбора формул для их описания. Примером может служить часть многочисленных уравнений роста. Однако с течением времени математика все чаще стала использоваться как средство моделирования. В основе такого использования математики лежит формирование системы представлений и гипотез о некотором круге биологических явлений. После того как исходная система представлений сформирована, привлекается формальный аппарат, позволяющий получить выводы и предсказания о возможном характере поведения, о возможных режимах функционирования данной биологической системы. Эти выводы и предсказания должны в принципе допускать экспериментальную проверку. В результате же проверочных экспериментов, в свою очередь, уточняется модель. При таком подходе математическая модель оказывается существенным инструментом теоретического исследования. Математические модели в указанном смысле слова отражают основные, существенные связи между явлениями, известные на данном этапе познания, и позволяют ставить разнообразные мысленные эксперименты, которые порой очень трудно или даже невозможно поставить прямо на изучаемом объекте.
Параллельно с накоплением биологических знаний идет усложнение математических методов, используемых в биологии, причем оно касается всех способов применения математики. Так, в области биометрии в последнее время все шире используются методы многомерных статистик. При описании эмпирического материала вместо элементарных функций сейчас часто используются дифференциальные или интегральные уравнения и т. д. Наиболее существенное изменение и усложнение применяемого в биологии математического аппарата произошло в области математического моделирования. По существу, основным средством математического моделирования еще в первой трети XX в. были дифференциальные и интегральные уравнения и теория вероятностей. В последние десятилетия в математике возник ряд новых направлений, связанных с изучением систем высокой степени сложности (теория автоматов, теория игр, динамическое программирование и т. д.). Можно указать на попытки использования в биологии матричных методов, теории групп, топологических методов и других средств современной математики.
В связи с усложнением математических средств, используемых в биологии, все более широкое применение находят вычислительные машины. Быстрота операций, совершаемых машинами, позволяет обрабатывать большое количество данных и открывает новые возможности для биологического эксперимента. При этом обработка данных может выполняться непосредственно в ходе опыта, так что исследователь получает необходимые результаты тогда, когда еще можно изменить направление эксперимента. Более того, вычислительная машина может сама по заданной программе вести эксперимент, меняя его ход в зависимости от получаемых результатов. Некоторые эксперименты, связанные с исследованиями быстро протекающих процессов, вообще принципиально невыполнимы без использования быстродействующих технических средств.
Еще большее значение имеют вычислительные машины для создания в биологии математических моделей. Биологические системы часто описываются нелинейными уравнениями, системами из большого числа дифференциальных уравнений или сложными логическими схемами, так что после формулировки основных положений анализ модели без использования вычислительной техники оказывается столь трудоемким, что она становится непродуктивной. Таким образом, наряду с появлением новых математических направлений принципиальную роль в математизации биологии стала играть и вычислительная техника.
Математические модели, основанные на использовании представлений физики и химии.
При рассмотрении разнообразных биологических вопросов, относящихся прежде всего к биофизике, биохимии и молекулярной биологии, возникают математические задачи, часто совпадающие с задачами теоретической физики или химии, либо весьма близкие к ним. Естественно, что модели, используемые при решении задач такого рода, наиболее строги и бесспорны, поскольку и основные понятия, необходимые при построении таких моделей, и соответствующий математический аппарат обычно достаточно хорошо апробированы на аналогичных физических задачах.
Одной из первых, в которой была построена математическая модель биологического явления, можно, считать упоминавшуюся выше работу Л. Эйлера (1730). В этой работе сердце рассматривается как насос, а кровеносная система — как система упругих трубок. В дальнейшем в работах по гемодинамике было дано объяснение многих явлений (например, пульсовой волны), хотя вследствие больших математических трудностей ряд вопросов функционирования системы кровообращения до сих пор не описан математически. Принципы механики были использованы в трудах О. Фишера (1895) по кинематике суставов, в работах по применению учения о сопротивлении материалов для объяснения структуры костной ткани, по изучению движений животных в различных средах, а также в исследованиях по физиологической акустике. Важные работы по математической биофизике были выполнены группой Н. Рашевского, которая работает в Чикагском университете (США) с 1934 г.
В пробуждении интереса к проблемам молекулярной биологии заметную роль сыграла книга Э. Шредингера (Нобелевская премия, 1933) «Что такое жизнь с точки зрения физики?» (1945). Значительная часть математических работ в области молекулярной биологии базируется на статической физике и термодинамике. Так, в книге Ф. Джонсона, Г. Эйринга и М. Полиссара «Кинетические основы молекулярной биологии» (1954) с этой точки зрения рассматривается перенос веществ через биологические мембраны, зависимость биолюминесценции от температуры, процесс мышечного сокращения и т. д. В книге М.В. Волькенштейна «Молекулы и жизнь» (1965) приведен обзор современных работ (в том числе математических моделей матричной редупликации ДНК, мышечного сокращения), основанных на теоретической физике.
В литературе обсуждается необходимость объяснения ряда биологических процессов на основе квантовой механики. Речь идет в первую очередь о процессах фотосинтеза, фотохимических процессах зрения, биолюминесценции и процессах ферментативного катализа.
Представления термодинамики используются не только при изучении биологических процессов, происходящих на атомно-молекулярном уровне; они находят применение и при изучении физиологических процессов, например, при исследовании терморегуляции. В развитии этого направления особое место занимает работа Э.С. Бауэра (1935).
Среди работ физико-математического направления выделяются исследования по электробиологии, в особенности касающиеся возникновения возбуждения в рецепторах и распространения нервного импульса. Изучением физико-математических аспектов процесса возбуждения занимался П.П. Лазарев. В работе «Ионная теория возбуждения» (1923) он рассматривал принципиальные вопросы построения математической биологии и выделил круг явлений, который успешно описывается при помощи физико-химических моделей (биомеханика, физиологическая оптика и т. д.). При этом он выражал уверенность, что в дальнейшем удастся создать модели и таких явлений, как рост, размножение и др.
Более 100 лет назад было установлено, что распространение возбуждения по нервным волокнам связано с возникновением электрического тока. Л. Герман в 1868 г. выдвинул теорию электрического распространения возбуждения, согласно которой возбужденный участок нервного волокна генерирует ток, который, действуя на соседний невозбужденный участок, делает его, в свою очередь, генератором тока. Как было показано в дальнейших исследованиях, роль генератора играет поверхностная структура нервного волокна — его мембрана (см. главу 11).
В 1952 г. А.Л. Ходжкин и Э.Ф. Хаксли предложили математическую модель для описания поведения мембраны нервного волокна и процесса распространения импульса (Нобелевская премия, 1963). В этой модели свойства мембранного генератора, определяющиеся проницаемостью мембраны для разных ионов, описываются системой линейных дифференциальных уравнений первого порядка. При описании процесса распространения нервного импульса они исходят из того, что по своей электрической структуре нервное волокно подобно кабелю; распространение моделируется мембранными уравнениями и кабельным уравнением. Таким образом, задача сводится к решению системы дифференциальных уравнений, одно из которых — нелинейное уравнение в частных производных. Детальное исследование этой модели удалось выполнить только в последние годы благодаря применению вычислительных машин.
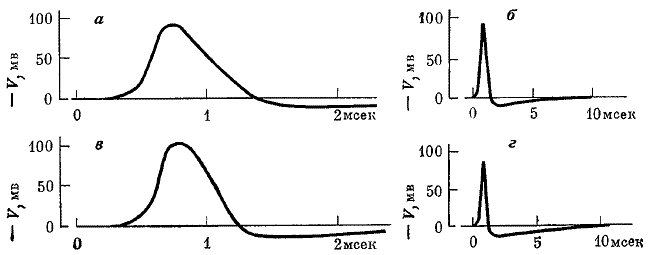
Сравнение теоретически вычисленных по уравнениям Ходжкина-Хаксли, (а, б) и полученных экспериментально (в, г) распространяющихся потенциалов действия в аксоне кальмара (по Ходжкину и Хаксли, 1952).
Вычисленная скорость — 18,8 м/сек; скорость в эксперименте — 21,2 м/сек.
Принципиальное значение модели Ходжкина-Хаксли состоит в том, что на основании описания немногих основных элементарных свойств мембраны нервного волокна удалось объяснить и предсказать целый ряд явлений, которые до того рассматривались как независимые. Так, была получена правильная форма потенциала действия, воспроизведены закономерности изменения сопротивления мембраны при возбуждении, объяснен смысл порогового потенциала и рефрактерного периода и даны их количественные оценки, описано явление аккомодации и т. д. В известном смысле, эта модель может служить образцом математических моделей: в ней на основании небольшого числа исходных постулатов количественно описано большое число явлений, которые до этого казались не связанными между собой. Она демонстрирует возможность описания широкого круга явлений при помощи небольшого числа определенных терминов. В этом отношении модель Ходжкина-Хаксли близка к моделям генетики или теоретической физики.
Большое практическое значение имеет вопрос об электрическом поле, создаваемом во внешней среде совокупностью нервных или мышечных клеток, возбуждающихся в определенной последовательности. С анализом этих полей связаны попытки объяснения характера кардиограмм, миограмм, электроэнцефалограмм, широко используемых в медицине. Разработка теории возникновения и методов объективного анализа этих электрических процессов является в настоящее время предметом исследований многих математиков и биологов.
Другое направление в изучении распространения возбуждения ведет свое начало от работы Н. Винера и А. Розенблюта (1946, русский перевод 1961). В ней рассмотрено распространение активности в некоторой идеальной возбудимой среде, свойства которой заданы аксиоматически. Авторы делают попытку выяснить условия возникновения в такой среде аномальных режимов, аналогичных фибрилляции сердца или эпилептическим разрядам в нейронной сети. Анализ идеальной возбудимой среды (с учетом возможности спонтанной активности ее точек) позволил И.М. Гельфанду и М.Л. Цетлину (1960) показать возможность существования в таких средах свойства, аналогичного памяти, а также объяснить некоторые особенности работы синусного узла сердца. В последнее время получили новое развитие работы по моделированию сердечных фибрилляций и по изучению распространения возбуждения в идеальных средах, свойства которых приближаются к свойствам реальных объектов, в частности, в разветвленных волокнах и синцитиях (Ю.И. Аршавский и др., 1966; М.Б. Беркинблит и др., 1966; Г. Моу, 1967; В.И. Кринский, 1968).
Концепции и представления теоретической химии, широко используемые в биологии для построения различных математических моделей, основаны главным образом на феноменологическом подходе, выдвинутом в 1945 г. английским химиком К.Н. Хиншельвудом (Нобелевская премия, 1956). Хиншельвуд предложил использовать для описания кинетики химических реакций, протекающих в клетке, систему нелинейных дифференциальных уравнений. К сожалению, при реализации такого подхода обычно не хватает биохимических данных о конкретных реакциях, идущих в интактной клетке. Тем не менее на этом пути уже достигнуты определенные успехи. Так была, например, построена модель разложения глюкозы на СО2 и Н2О. Для описания этой реакции с достаточно полным использованием биохимических данных потребовалось исследовать систему из 21 дифференциального уравнения. В результате анализа были получены графики зависимости концентрации разных компонентов от времени. Проведенный анализ позволил оценить правильность существующих представлений о ходе этой реакции (А. Парди, 1962).
При исследовании системы нескольких десятков дифференциальных уравнений вычислительные машины становятся незаменимыми. Если же рассматривать не изолированную реакцию, а систему реакций, в результате которых в клетке синтезируются сотни веществ, влияющий друг на друга, то получается очень сложная многоконтурная система с множеством обратных связей. Для описания такой системы требуются тысячи уравнений. Несмотря на указанные трудности, подход, предложенный Хиншельвудом, продолжает развиваться, что, в частности, позволило показать возможность возникновения колебательных режимов для химических реакций и выяснить условия возникновения таких режимов[243]. Колебательные процессы в организме представляют большой интерес в связи с проблемой «биологических часов». Этой проблеме в последнее время посвящено большое количество работ, во многих из которых содержатся математические модели[244].
Использование в биологии теории информации.
Разработка теорий информации связана с работами Р. Хартли, В.А. Котельникова, А.Н. Колмогорова, К. Шеннона, А.Я. Хинчина и других. Вместе с этой теорией в науку вошли такие понятия, как количество информации, пропускная способность канала передачи информации, кодирование и декодирование информации и другие.
Универсальность этих понятий привела к тому, что информационный подход начал широко применяться и к биологическим проблемам. Большую роль в постановке биолого-информационных проблем сыграли работы А.А. Ляпунова, сформулировавшего ряд задач, относящихся к исследованиям в области управления в биологических системах. С позиции теории информации в настоящее время рассматриваются процессы, протекающие в отдельных клетках, в организмах и в популяциях. Особенно плодотворным оказался информационный подход при изучении работы органов чувств и мозга. Возник и разрабатывается ряд проблем, связанных с выяснением принципов обеспечения помехоустойчивости и надежности элементов, осуществляющих переработку, передачу и хранение информации. С этих же позиций рассматриваются в настоящее время процессы коммуникации между животными, способы решения ими задач ориентации, навигации и локации, проблема памяти и другие проблемы, относящиеся к компетенции бионики.
Одним из наиболее фундаментальных результатов, определяющим в значительной мере состояние современной биологии и связанным с информационным подходом, является расшифровка генетического кода (см. также главы 23 и 24). Впервые эта проблема была, по-видимому, сформулирована Э. Шредингером (1945), который мог поставить ее лишь в общей форме, так как тогда еще не была известна структура ДНК и ее генетическая роль.
Строгая и конкретная постановка и анализ задачи о генетическом коде связаны с исследованиями Г. Гамова (1954). Задача состояла в выяснении соответствия между последовательностями нуклеотидов в молекуле ДНК и последовательностью аминокислот в белках.
Гамов подошел к этой проблеме как к задаче расшифровки текста, использовав ряд простых соображений комбинаторики. Так, совершенно ясно, что один нуклеотид не может определять одну аминокислоту, поскольку нуклеотидов всего 4, а аминокислот — 20. Точно так же не годится код, при котором аминокислоты кодируются последовательностью двух нуклеотидов, так как число сочетаний из четырех по два всего 16. Отсюда первый вывод — генетический код реализуется по крайней мере трехчленными сочетаниями, как это в дальнейшем и было установлено. Однако число сочетаний из четырех по три равно 64 и для 20 аминокислот оно слишком велико. Отсюда было сделано заключение об Избыточности кода и о существовании бессмысленных триплетов. Через семь лет после появления работы Гамова Ф. Крик, Дж. Уотсон, М. Ниренберг и другие, расшифровали генетический код. Влияние теоретико-информационного подхода, подготовившего решение этой проблемы, сказалось даже в терминологии (генетический код, информационная РНК и т. д.).
Информационный подход существен и для понимания других процессов, связанных с поведением и взаимодействием клеток, например, при заживлении ран, регенерации и т. д. При изучении иммунитета встают вопросы о том, как осуществляется процесс «узнавания» своих белков, каким образом чужеродный белок, побывавший в организме всего один раз, «запоминается» на всю жизнь, какое количество разных чужих белков может быть распознано и т. д. Все эти вопросы связаны с проникновением в биологию идей теории информаций.
Вероятно, наибольшее воздействие теория информации оказала на разделы физиологии, изучающие органы чувств и нервную систему. Исследование принципов переработки информации является здесь основным направлением экспериментальных работ. Физиологи в настоящее время интенсивно изучают способы кодирования сигналов об интенсивности света и звука, о цвете или частоте тона, процессы адаптации, явление константности восприятия и т. д. В связи с изучением работы рецепторов и нервной системы было предложено много моделей, имитирующих принципиальные стороны или механизмы процесса переработки информации нейронами. Значительную часть таких моделей составляют так называемые нервные сети.
Начало изучению нервных сетей было положено работой У.С. Мак-Каллока и В. Питтса (1943). Эти авторы рассматривали сети, образованные пороговыми элементами, которые могут находиться только в одном из двух состояний «включено» или «выключено». Они пришли к выводу, что любая функция нервной системы, которая поддается логическому описанию при помощи конечного числа слов, может быть реализована формальной нервной сетью. Тем самым была показана принципиальная возможность моделирования любых формализуемых функций мозга. В этой работе использовалась крайне упрощенная модель нейрона: принималось, что порог нейрона не меняется во времени и что срабатывание любого тормозного синапса полностью затормаживает нейрон. В дальнейшем в теории нервных сетей перешли к рассмотрению структур, образуемых элементами, свойства которых близки к свойствам реальных нейронов.
Физиологические исследования последних лет показали, что органы чувств животных, как правило, не являются простой мозаикой рецепторов, каждый из которых независимо реагирует на свет или темноту, звук или его прекращение и т. д. Оказалось, что уже на уровне органов чувств существуют специальные структуры («детекторы»), которые могут выделять контуры изображения, углы, движущиеся предметы и т. д. Существенно, что эти операции осуществляются в органах чувств не в результате обучения, а вследствие самой конструкции органа, выработанной в процессе эволюции. Моделированию сетей, которые выделяют только определенные группы внешних сигналов или определенные признаки, посвящена большая серия работ.
Б?льшая часть моделей этого типа соответствует специализированным нервным сетям с детерминированными связями. Структура такой сети, топология ее связей специально приспособлена для решения определенной задачи. Г.Д. Ландаль (1962) рассмотрел сети, которые реагируют только на движущиеся объекты, а также сети для оценки кривизны траектории движущегося объекта и восприятия цвета. Специально рассматривались механизмы, которые могут обеспечить неизменность реакции при разных размерах, смещениях и поворотах воспринимаемого образа (У Мак-Каллок, В. Питтс, 1947; Н. Винер, 1948; Дж. Т. Калбертсон, 1950).
Одной из существенных особенностей работы сетей для обработки сигналов является латеральное торможение. Это явление, подробно исследованное на сетчатке глаза мечехвоста, состоит в том, что нейроны одного и того же слоя при действии на них сигналов тормозят друг друга тем сильнее, чем ближе друг к другу располагаются. Наличие латерального торможения было затем установлено в сетчатке глаза, в слуховой системе, системе осязания и в некоторых других структурах центральной нервной системы позвоночных. Количественную модель для преобразования изображений глазом мечехвоста предложил В. Рейхардт (1965). Он выяснил, в какой мере боковое торможение исправляет недостатки оптической системы этого глаза. Использование таких сетей для анализа акустических образов было предложено П. Мюллером, Т. Мартином и Ф. Путцратом (1962) и подробно исследовано в модели слуховой системы Н.В. Позиным (1970).
Наряду с системами, анализирующими поступающие сигналы, изучались также сети, решающие обратную задачу — формирование выходных команд для исполнительных органов. В частности, рассматривались сети, обеспечивающие возникновение периодической активности нервных клеток и мышц — модели дыхания, ходьбы, полета, модели, обеспечивающие асинхронную работу мотонейронов и другие (И.М. Гельфанд и др., 1963; Н.В. Позин, 1970).
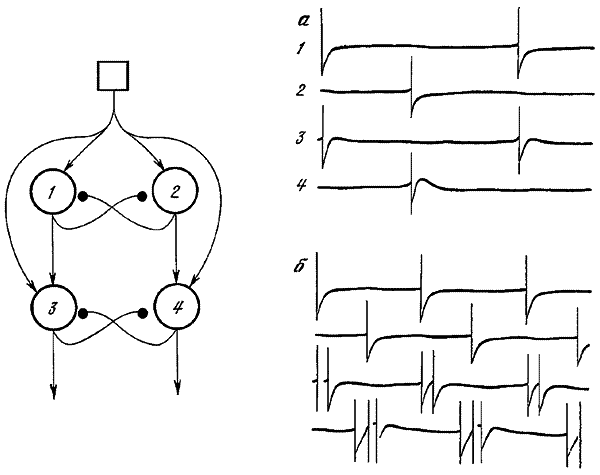
Простая нейронная сеть, моделирующая работу летательной системы саранчи (по Д. Вилсону и И. Уолдрон, 1968).
Сеть состоит из четырех нейронов. Зачерненными кружками обозначены тормозные синапсы стрелками — возбуждающие; Показан характер импульсной активности в разных нейронах сети; а и б соответствуют разным уровням входного потока.
Помимо вопросов о принципах хранения, передачи и переработки сигналов теория информации занимается также проблемами надежности и борьбы с шумами. Эти проблемы возникли в технике Связи, при конструировании вычислительных машин и сложных комплексов, где большое число используемых элементов увеличивало вероятность получения ошибочных результатов. В качестве биологической проблемы вопрос о надежности мозга был поставлен еще опытами К. Лешли (1918–1933).
В математическую форму проблема надежности была облечена Дж. фон Нейманом (1952) и впервые рассмотрена им, а также Е. Муром и К. Шенноном (1956). Один из методов Повышения надежности, предложенный Нейманом, состоял в том, что выход каждого элемента заменялся пучком линии, а каждый элемент сети — схемой, которая оперировала с пучками входных и выходных; линий. Нейман оценил избыточность схемы, необходимую для достижения определенной надежности. Например, если вместо одного элемента, который ошибается один раз из 200, использовать 60 000 элементов, то ошибка будет возникать один раз на 1020 случаев.
Мур и Шеннон отметили связь задачи, рассмотренной Нейманом, с проблемой построения надежного кода для случаев, когда надежность передачи отдельного символа низка. Они показали, что при использовании других элементов схемы могут быть получены лучшие результаты и обеспечено то же повышение надежности при избыточности не в 60 000, а всего в 100 раз.
Одна из самых слабых сторон нервных сетей, подобных рассмотренным Мак-Каллоком и Питтсом, — их крайне низкая надежность: выход из строя всего одного нейрона может принципиально изменить характер работы всей сети. В 1958 г. Мак-Каллок предложил усложненную модель формального нейрона. В ней учтено, что порог нейрона может меняться во времени, принят закон суммации возбуждающих и тормозных входов, более близкий к реальному (возбуждение наступает, когда алгебраическая сумма входных сигналов превышает пороговое значение), а также учитывается существование пресинаптического торможения, т. е. используются входные волокна, которые могут блокировать прохождение сигнала по другим входам. С использованием этих элементов был рассмотрен ряд вопросов о конструировании сетей, устойчивых к шуму (У. Мак-Каллок, Дж. Коуэн, Л. Вербик и др., 1960). Была решена задача о синтезе сетей, работа которых не меняется, когда порог всех нейронов одновременно сдвигается на одну или несколько единиц (логически стабильные сети). Поясняя значение этой модели, Мак-Каллок отмечает, что дыхание не прекращается и при таких стадиях наркоза, когда пороги раздражения нейронов увеличиваются вдвое.
Далее были исследованы возможность и методы построения нейронных сетей, которые работают без ошибок при неодновременных и даже разнонаправленных сдвигах порогов образующих их элементов, а также при изменении веса синапсов, появлении новых связей между нейронами и при некоторой вероятности того, что нейрон не ответит на сверхпороговый сигнал или, напротив, самопроизвольно возбудится в отсутствие входного сигнала. При этом возникает задача построения сетей такого рода с использованием минимального числа нейронов и связей — задача во многих случаях еще далека от решения.
Постановка проблемы надежности привела к новому подходу ко многим вопросам биологии. И.И. Шмальгаузен (1958–1963), например, рассмотрел под этим углом зрения полигены (повторение генов со сходным выражением), диплоидность и полиплоидность организмов и т. п. Им затронут также вопрос о циркуляции информации в процессе смены поколений и в эволюции. Работами Шмальгаузена была установлена связь дарвиновской теории эволюции с теорией информации.
Теория управления и биология.
В конце XIX и начале XX в. в математике стала усиленно развиваться теория динамических систем, возникшая на основе теории дифференциальных уравнений. В технике этому соответствовала разработка теории автоматического управления (регулирования). Одним из фундаментальных положений этой теории явилось понятие «обратной связи» и формулирование принципа управления по отклонению фактического состояния управляемого объекта от заданного. Развитие теории информации и статистических методов исследования управляющих систем позволило Н. Винеру (1948) сформулировать ряд положений о единстве принципов управления в технических системах и живых организмах: было установлено наличие и большое значение обратной связи и управления по рассогласованию в биологических системах, а также информационный характер процессов регулирования и управления в биологии.

Норверт Винер. 1895–1964.
Понятие обратной связи, впервые систематически использованное применительно к биологическим системам Винером, в качественной форме складывалось раньше. Его можно встретить в ряде биологических работ, посвященных изучению регуляторных процессов и механизмов [Н.А. Белов, 1911; сенсорная коррекция, Н.А. Бернштейн, 1934; обратная афферентация, П.К. Анохин, 1935 (Ленинская премия, 1972); «плюс-минус взаимодействие», М.М. Завадовский, 1941[245]; и др.].
Широта и общность понятия обратной связи привели к проникновению в биологию методов анализа систем регулирования и способствовали бурному развитию биологических областей, в которых применимо моделирование. О степени проникновения идей управления в биологию можно судить по попыткам использовать понятие обратной связи и управления для формального описания понятия жизнь и живое (А.А. Ляпунов и С.Л. Соболев, Н.В. Тимофеев-Ресовский), показавшим, что любая живая система может рассматриваться как сложная иерархическая система управления, обеспечивающая сохранение и поддержание множества параметров, точно определяющих существование живого объекта и его целостность.
Подход к биологическим системам с позиций теории управления привел к появлению большой серии исследований по изучению частотных характеристик отдельных биологических регуляторных систем, по выявлению конкретных морфологических основ реализации обратных связей и обеспечения надежности передачи информации, необходимой для управления, по изучению устойчивости, точности и помехозащищенности этих систем. Вот некоторые направления исследований, связанные с проблемой управления в биологических системах.
Процессы регуляции в клетке.
Изучение поведения клеток в организме и в культуре ткани позволило обнаружить в них разнообразные регуляторные процессы, а также влияние внешних факторов на деление и движение клеток, синтез тех или иных продуктов и т. д. Наиболее детально изучен в настоящее время процесс регуляции синтеза ферментов в бактериальных клетках. Полученные результаты позволили Ф. Жакобу и Ж. Моно (1961) предложить модель регуляции, основанную на представлении о положительной и отрицательной обратной связи (см. главу 23). При появлении в клетке некоторых питательных веществ начинается энергичный синтез ферментов, необходимых для их обработки. Этот процесс идет по принципу положительной обратной связи. Напротив, при избытке конечных продуктов некоторых реакций происходит репрессия — подавление синтеза ферментов, необходимых для образования этих продуктов. Жакоб и Моно показали, что регуляция синтеза осуществляется особыми генами-операторами, вырабатывающими специфические белковые вещества, которые играют роль регулирующих сигналов. В ряде случаев показано, что этот процесс дублируется другой параллельной системой регуляции, которая связана не с полным блокированием синтеза ферментов, а с изменением их активности. При этом избыток конечного продукта снижает активность фермента, катализирующего первую реакцию в цепи биосинтеза данного продукта. Известны реакции, в которых, напротив, активность фермента повышается. Наличие двух независимых систем регуляции существенно повышает надежность работы всей системы. Таким образом, эта наиболее обоснованная схема регуляции синтеза ферментов аналогична техническим системам регуляции.
Моделирование самовоспроизведения.
Один из важнейших биологических процессов, идущий самопроизвольно или индуцируемый внешними воздействиями, — процесс клеточного деления. При этом процессе идут многочисленные реакции синтеза, удвоения клеточных структур, совершаются механические перемещения, приводящие к обособлению дочерних клеток. Для описания этого процесса, являющегося одной из наиболее характерных особенностей живых систем, было предложено несколько математических моделей.
Дж. Нейман (1951) впервые изучил два варианта таких моделей. Первая модель была кинематической: она представляла собой автомат, состоящий из элементов, расположенных в пространстве, например, из датчика, который позволяет обнаруживать присутствие других деталей, соединительных частей для скрепления этих деталей и т. д.; при этом такой автомат реально не конструировался, а только рассматривался логически. Предполагалось, что он плавает в резервуаре, в котором находится неограниченный запас деталей (подобно тому, как клетка в культуре ткани окружена питательной средой). Нейман показал, что может быть создана машина с программой, которая будет собирать подобные себе автоматы и копировать для них свою программу.
Вторая модель Неймана проще и носит абстрактный характер. Она представляет собой бесконечную решетку (подобную шахматной, доске), каждый квадрат которой может находиться в некотором числе состояний (в модели Неймана их 29). Состояние любой клетки в данный момент зависит от ее состояния в предыдущий момент и от состояния четырех соседних клеток. На этой решетке при соответствующем начальном состоянии можно получить конфигурации, которые сохраняются, двигаются по решетке и порождают подобные себе. Эти работы были продолжены Э.Ф. Муром (1959), М. Арбибом (1965) и рядом других.
Шведский исследователь Л. Лофгрен (1958), рассматривая автоматы, способные обнаруживать ошибки и заменять испортившиеся детали (самовосстанавливающиеся автоматы), связывает надежность с самовоспроизведением. Такие автоматы можно рассматривать как модели регенерации.
Нейман отмечал, что программа его самовоспроизводящихся автоматов подобна клеточному геному, а построение нового автомата, аналогичного исходному, — процессу дупликации генетического материала. С этой точки зрения, ошибки в программе нового автомата, возникающие при ее переписывании, — аналог генетических мутаций. Нейман показал, что для самовоспроизводящихся автоматов существует некоторый критический размер. Автоматы, имеющие размеры меньше критического, могут порождать только более простые, чем они сами. Автоматы большего размера могут порождать подобные себе или даже более сложные.
Таким образом, при некотором уровне сложности системы возникает предпосылка для дальнейшей самостоятельной эволюции автоматов и их приспособления к среде.
Модели межклеточного взаимодействия и формообразования.
Проблема развития занимает в современной биологии одно из центральных мест. Вопросы о механизмах реализации генетической программы в онтогенезе (дифференцировка тканей, возникновение органов) интенсивно изучаются как экспериментально, так и теоретически. Трудности, стоящие перед этой проблемой, того же порядка, что и при изучении клеточной регуляции: они определяются очень большим числом элементов, взаимодействующих между собой. Поэтому предложенные до настоящего времени модели морфогенеза рассматривают, как правило, его отдельные стороны или свойства.
По-видимому, впервые вопросы роста и формообразования с позиций геометрии анализируются в книге А.У. Томпсона «О росте и форме» (1917), где рассматривается расположение листьев на ветке, форма рогов, яиц, раковин и т. д. Особенности формы некоторых структур и их возникновение в процессе морфогенеза пытался объяснить А.Г. Гурвич теорией биологического поля (1922–1944), идеи которой получили дальнейшее развитие в работах Л.В. Белоусова (1970) (см. главу 14). Из современных можно отметить работы Р. Тома (1968), основанные на топологических представлениях.
Одна из первых неформальных моделей морфогенеза была предложена в 1952 г. А. Тьюрингом. Он показал, как группа одинаковых клеток, имеющая симметричную форму, например сферическую, может развиться в более сложную структуру. Кроме того, он выяснил, как из клеточного кольца может возникнуть фигура с тремя или четырьмя лепестками.

Джон фон Нейман. 1903–1957.
Другая группа моделей, основанных на анализе взаимодействия автоматов, имитирует устойчивость эмбриогенеза. В частности, рассмотрены группы взаимодействующих автоматов, образующих некоторую дифференцированную структуру, в которой при удалении части этих автоматов оставшиеся вновь образуют такую же структуру, только меньшего размера (М.Л. Цетлин, 1964; Л. Вольперт, 1968; М. Аптер, 1970).
Сопоставление взаимодействия между клетками в процессе их развития с взаимодействием в группе автоматов позволяет сделать некоторые выводы принципиального характера. Регуляция в подобной группе должна осуществляться за счет локального взаимодействия автоматов, так как в системе отсутствует единый центр, который рассылал бы команды всем компонентам группы. Модели децентрализованного управления, когда общая задача всей системы решается за счет локальных взаимодействий ее элементов, представляют большой интерес не только для описания процессов эмбриогенеза, но и для биологии в целом, так как они одинаково касаются процессов регуляции в клетке, в организме и в популяциях. Это пример моделей, создание которых вызвано не техникой, а биологией. Подобные модели изучались И. М. Гельфандом, М.Л. Цетлиным (1966), а также Д. Мичи и Р. Чемберсом (1968).
Регуляция функциональных процессов в организме.
Проникновение в биологию идей теории управления, пожалуй, в наибольшей степени повлияло на изучение физиологических процессов у животных. Появилось большое количество работ, в которых с позиций автоматического регулирования были исследованы особенности регулирования в системах кровообращения и дыхания, поддержания равновесия, регулирования содержания сахара в крови, работы глазодвигательной системы, регулирования температуры тела и т. д. С этой же точки зрения были изучены и некоторые простейшие формы поведения, например, оптокинетические реакции насекомых[246].
Использование принципов регуляции стимулировало постановку новых экспериментов и в ряде случаев привело к лучшему пониманию работы биологических систем. Так, на основе анализа регулирования размеров зрачка был поставлен следующий изящный эксперимент. Пучок света направлялся на зрачок так, что одна его часть попадала внутрь зрачка, а другая проходила за его пределами. Сушение зрачка в этом случае приводит к снижению интенсивности света, попадающего в глаз, вследствие чего он вновь расширяется, пропуская большее количество лучей. Испытуемый ощущает при этом только периодические колебания интенсивности света.
Анализ процессов управления в физиологических системах показал, что эти системы почти всегда оказываются многоконтурными и содержат много параллельно работающих цепей и обратных связей. Возникающие при этом трудности аналогичны трудностям анализа системы биохимических реакций в клетке и межклеточных взаимодействий.
В настоящее время выдвинут ряд принципов, позволяющих в какой-то мере обойти указанные трудности. Так, еще Н.А. Бернштейн (1947) сформулировал задачу управления движениями как борьбу с лишними степенями свободы. В работах И.М. Гельфанда и других (1966) было показано, что при решении той или иной задачи степени свободы оказываются связанными между собой, и ими можно управлять как единым целым. При этом некоторая группа мышц и суставов объединяется в более или менее автономный блок.
Другой важный принцип управления сложными системами — иерархическая структура системы управления. Применительно к проблеме координации движений этот принцип был подробно обоснован Н.А. Бернштейном (1947). Преимущества иерархической структуры были рассмотрены также А.А. Ляпуновым (1963).
Таким образом, вырабатывается новая система понятий, характерных для биологических систем управления — блочный принцип управления, иерархичность структуры управления, достижение цели за счет локального взаимодействия элементов и т. д.[247] Вместе с тем поднимаются и новые, пока еще нерешенные вопросы, в частности, вопрос о том, каким образом одна и та же система при помощи одних и тех же исполнительных механизмов может решать большое количество разнообразных задач.
Моделирование взаимоотношений организма со средой. Математическая психология.
Исследованиям целостного поведения живых систем положили начало работы по изучению внешних проявлений процесса обучения и связанного с ним рефлекторного поведения.
В 50-х годах XX в. Г. Уолтер, А. Оэттингер и др.[248] разработали ряд моделей условно-рефлекторного поведения, воспроизводящих явления обучения и забывания при выработке простейших условных рефлексов. Эти модели дали возможность установить перечень необходимых функциональных элементов, которыми должна располагать система для реализации этого вида деятельности, и послужили прототипами при создании простых технических адаптивных систем.
Первая модель, позволившая упрощенно воспроизвести и изучить возможные нейронные механизмы обучения, была разработана в 1954 г. американцами Б.Дж. Фэрли и У.А. Кларком. Это была математическая модель нервной сети, изучавшаяся при помощи электронной вычислительной машины. Модель представляла собой сеть нейронов со случайными связями, которые должны были при внешнем возбуждении определенной группы входных нейронов вызвать систематическое возбуждение определенной группы выходных нейронов. Требуемое состояние достигалось в процессе обучения путем изменения эффективности межнейронных связей и порогов возбуждения нейронов. Значение работы Фэрли и Кларка заключалось и в том, что она породила целую серию дальнейших исследований, основанных на представлении об обучающихся нейронных сетях.
Р. Бёрль (1956) рассмотрел нейронную сеть со случайными связями, по которой могут распространяться незатухающие волны. Оказалось, что в области, через которую идет волна, возбуждаются лишь нейроны с наиболее низким порогом. Если волны возникают в двух точках (совпадение во времени двух раздражителей), то в сети появляется область пересечения двух волн, в которой за счет суммации могут возбудиться и нейроны с более высоким порогом раздражения. Приняв, что чувствительность клеток после срабатывания в течение некоторого времени остается повышенной (свойство, эквивалентное проторению путей), удается после нескольких сочетаний обоих раздражителей применением только одного из них породить в среде волну, соответствующую второму. Снижение порогов после возбуждения является, по Берлю, тем механизмом памяти, который обеспечивает обучение и его частный случай — выработку условных рефлексов.
Другая модель выработки условных рефлексов, классификации раздражителей и обучения была предложена А.М. Аттли (1956). Процесс обучения в ней реализуется путем вычисления условных вероятностей. Аттли считал, что многочисленные связи между элементами, необходимые для работы модели, возникают случайно. С 1957 г. начала выходить серия работ Ф. Розенблатта, посвященная использованию для узнавания образов сетей со случайными связями между элементами, эффективность действия которых друг на друга изменяется в результате обучения. Подобные системы вслед за Розенблаттом стали называть перцептронами.
В рамках общей проблемы обучения вопросы узнавания (распознавания) образов занимают особое место. К задаче узнавания сводится большое число психических функций, таких, как принятие решений, требующее распознавания ситуации, проблема обобщения и выработки понятий, также связанная с узнаванием и различением. Эти вопросы затрагиваются в многочисленных исследованиях.
Задачи распознавания образов выходят за пределы чисто биологических исследований и в настоящее время тесно смыкаются с техническими (бионическими) проблемами конструирования различных распознающих систем и устройств (для чтения текстов, восприятия речи, автоматического диагноза, анализа крови и т. п.).
Значение перцептронов состоит еще и в том, что они являются одной из первых моделей распознающей системы, не содержащей врожденных, «жестких» механизмов классификации и способной обучаться распознаванию различных образов из довольно широкого класса. В основе схемы перцептрона лежат идеи модели Фэрли и Кларка, дополненные представлениями о слоистой структуре сетчатки. Первый слой образуют рецепторные элементы, случайно связанные с элементами второго слоя — ассоциативными, которые воздействуют на элементы третьего слоя — выходные. После проекции образа на слой рецепторов срабатывает какой-то из выходных элементов. Бели он соответствует образу, который действовал на рецепторы, то эффективность связей, которые были при этом активированы, возрастает; в случае ошибки эффективность сработавших связей ослабевает.
В работах Ф. Розенблатта (1959), В.М. Глушкова (1962) и других были выяснены реальные возможности и недостатки трехслойных перцептронов. Исследовались также и более сложные многослойные перцептроны с возвратными связями. Одним из принципиальных недостатков перцептрона, обусловленных наличием большого числа случайных связей между элементами, является довольно медленное обучение. Впрочем, эта же конструктивная особенность обеспечивает их надежность: выход из строя нескольких элементов перцептрона на качестве его работы сказывается незначительно.
Важное направление в теории сетей, моделирующих деятельность мозга, развивается в последние годы Г. Бриндли и Д. Марром (1969).
Процесс обучения можно анализировать и с иной точки зрения. Так, в работах Р. Буша и Ф. Мостеллера (1955), Р. Аткинсона, Г. Бауэра и Э. Кротерса (1965) обучение рассматривается как некоторый стохастический процесс анализа ситуаций и выбора решений. Их исследования базируются на попытках формального анализа психологических особенностей обучения и образуют комплекс, получивший название математической психологии. В этой области также построен ряд интересных математических моделей.
Всякая модель обучения рассматривает взаимодействие обучающейся конструкции (сети, автомата, программы) и внешней среды. М.Л. Цетлиным (1961) предложена и проанализирована модель обучения конечного автомата в случайной среде. Биологическим аналогом процесса такого рода может быть обучение животного в Т-образном лабиринте, когда за поворот вправо и влево животное штрафуется случайным образом с разными вероятностями. Цетлин предложил простую конструкцию автомата, который обучается вести себя в таких условиях оптимальным образом. В его работах рассмотрен ряд примеров коллективного поведения простейших автоматов и показано, что системы из достаточно простых элементов, обладающих небольшими возможностями, способны реализовать достаточно сложные формы «целесообразного» поведения.
Важное значение в организации и управлении поведением имеют механизмы предсказания, учитывающие характер изменения ситуации. Концептуальной моделью такого механизма (предиктора) является положение об «акцепторе действия» П.К. Анохина (1933). В работе Л.В. Крушинского (1966) и других авторов предложена модель экстраполяционного рефлекса как одного из видов прогнозирующего поведения.
Н.А. Бернштейн (1961) подробно разработал идею, согласно которой люди в процессе деятельности, а животные в процессе жизни формируют в мозгу некоторую модель внешнего мира, содержащую, в частности, план будущего поведения. Эта модель развивается по мере приобретения опыта.
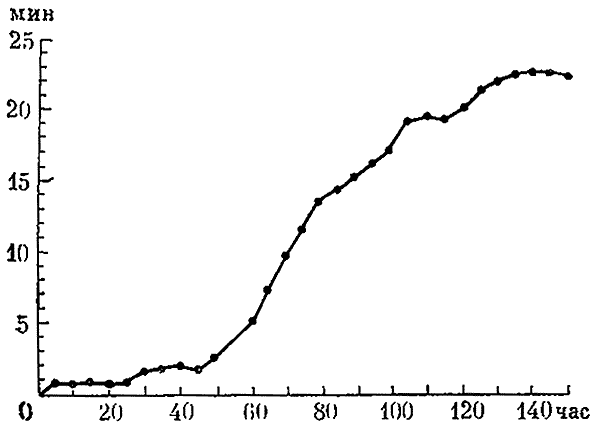
Кривая обучения коллектива автоматов (по Д. Мичи и Ф. Чемберсу, 1968).
По оси ординат — время до совершения ошибки, по оси абсцисс — время обучения системы.
В последние десятилетия активно ведутся работы по исследованию эвристической деятельности, т. е. процесса поиска нового или принятия решения при неполноте информации о среде. Моделирование здесь используется прежде всего для воспроизведения функции мышления при решении отдельных классов интеллектуальных задач[249].
Дж. Лоулином (1962) была предпринята попытка создания обучающейся программы, моделирующей некоторые типологические особенности личности, в частности, эмоции (желания, страх и гнев), от которых зависит поведение (приближение к объекту, убегание, нападение). Кроме того, поведение модели зависит от прошлого опыта: в зависимости от ее поступков в той или иной ситуации она получает приятные, неприятные или безразличные ощущения. Варьируя систему обучения, экспериментатору удалось получить на одной и той же модели два различных вида поведения — пассивное (трусливое), когда модель старалась избегать нового «риска», и активное (агрессивное), при котором модель искала новые ситуации и не боялась риска. Были проведены эксперименты по переучиванию такой модели при переходе из дружественной среды во враждебную и наоборот[250].
Математические модели в генетике популяции и в теории эволюции.
Эволюционный процесс можно рассматривать как процесс видового обучения или как процесс поиска оптимального состояния. При этом популяция выступает как регулируемая многопараметрическая система. Кроме того, эволюция может рассматриваться и как процесс группового поведения автоматов. С этой точки зрения, популяция — это совокупность «автоматов» (организмов), которые, взаимодействуя между, собой и с внешней средой, решают свои собственные локальные задачи. Однако в результате такого взаимодействия система в целом решает некоторую интегральную задачу, например, приспособления вида к новой среде обитания. Ясно, что в данном случае речь идет о примере управления за счет локальных взаимодействий, так как у популяции нет централизованного управляющего механизма. Математическая теория эволюции развивалась независимо от теории управления на основе собственных задач и методов (дифференциальные уравнения, теория случайных процессов).
Математическое исследование генетики популяций является одним из важнейших направлений современной теоретической биологии. Основы математической теории генетики популяций были заложены работами Г. Дженингса (1914–1917), С. Райта (1921–1932), Дж. Холдейна (1924–1932) и Р. Фишера (1928, 1930). Классическая работа в этой области принадлежит С.С. Четверикову (1926). В общей форме возникающая здесь задача может быть сформулирована так. Допустим, что данная популяция животных характеризуется определенным распределением генотипов и разной частотой встречаемости тех или иных признаков. Задан характер скрещивания в популяции и относительная жизнеспособность носителей этих признаков при тех или иных условиях. Требуется найти, как изменится в последующих поколениях распределение признаков при существовании популяции в данной (неизменной или меняющейся по определенному закону) среде. Простейший случай такой эволюционной задачи — вопрос о том, с какой скоростью будет происходить вытеснение некоторого исходного гена его аллелем, возникшим в результате мутации и имеющим селекционное преимущество. Основными факторами, влияющими на этот процесс, является частота мутирования и эффективность отбора. Фишер и Райт выяснили также роль размеров популяции и ограничения скрещивания внутри нее. Райт, кроме того, изучал влияние миграций. Роли миграций в изменении генофонда популяций посвящена работа А.Н. Колмогорова, И.Г. Петровского и Н.С. Пискунова (1937). А.Н. Колмогоров (1935) установил также отклонение от формулы Харди-Вейнберга в условиях ограниченного скрещивания, показав, что существует оптимум частичной изоляции, при котором скорость отбора максимальна. Качественные соображения о существовании такого оптимума были развиты А.А. Малиновским (1934).
Можно привести числовой пример, иллюстрирующий роль размеров популяция в эволюции, выявленную на моделях такого типа. Фишер показал, что если частота возникновения мутации 1/1 000 000, а ее селективное преимущество 1/100, то такая мутация будет закреплена в популяции из 10 000 000 особей уже через 25 поколений. В популяции же из 10 000 особей для этого потребуется 25 000 поколений — срок, за время которого мутация может утратить свою адаптивную ценность.
Идеи Холдейна, Фишера и Райта за последние годы получили развитие в разнообразных направлениях. Так, в работах Н.В. Тимофеева-Ресовского и Ю.М. Свирежева (1966) установлены механизмы, ведущие к устойчивому существованию полиморфных популяций, а в работах О.С. Кулагиной и А.А. Ляпунова (1966) рассмотрены механизмы дивергенции форм в популяциях.
Разработка математических вопросов генетики популяций интенсивно ведется за рубежом. В ряде работ изучен процесс эволюции при разных вариантах скрещивания, с учетом взаимодействия генов между собой, возрастного и полового состава популяции и т. д. Новое интересное направление развивает в последнее время японский ученый М. Кимура. Он проводит аналогию между эволюцией популяции и движением некоторой динамической системы, а затем, используя эту аналогию, стремится найти для описания эволюции принцип, аналогичный принципу наименьшего действия аналитической механики[251].
Математические модели в экологии. Модели биогеоценозов.
Если популяция, объединяющая особей одного вида, является основным объектом математической генетики популяций, то основным объектом теоретической экологии служат сообщества разных видов животных и растений вместе с той физико-географической обстановкой, в которой они живут. Основная задача, возникающая перед исследователем в этой области — предсказание динамики численности видов, образующих биоценоз.
Достаточно сложная экологическая система, содержащая много видов, естественно оказывается системой с большим числом параметров; поэтому при ее моделировании исследователь сталкивается с теми же трудностями, какие существуют и в других областях биологии. Для исследования систем из большого числа описывающих их уравнений в теоретической экологии в последнее время все чаще применяются цифровые вычислительные машины.
Проблемы, возникающие при исследовании биоценозов, представляют для экологов и эволюционистов не только теоретический интерес. Построение соответствующей математической теории призвано дать ответ на ряд практически важных вопросов: прогнозирование численности промысловых животных и вредителей сельского хозяйства, допустимые нормы отлова и отстрела, вопросы оптимального использования природных ресурсов и охраны природы и др.
Начало применению математических методов в экологии было положено исследованиями А. Лотки (1924) и В. Вольтерры с сотрудниками (1926 и позднее) (см. также главу 17). В них рассматривалась динамика численности двух или нескольких видов, которая описывалась, как правило, системой нелинейных обыкновенных дифференциальных уравнений; число последних соответствовало количеству взаимодействующих видов. Исследование систем уравнений показало, что в группе из нескольких видов могут возникать периодические колебания численности («волны жизни»), были определены условия полного вымирания одного из видов и т. д. Естественно, что подобные модели по необходимости носят весьма упрощенный характер.
Вольтерра рассматривал и более сложные варианты моделей, в которых учитывались процессы внутривидовой конкуренции, влияние питания в предыдущий период и т. д. Исследования взаимоотношений двух видов с учетом ряда факторов были выполнены в 30-х годах в СССР П.Ф. Гаузе и В.В. Алпатовым на модельных популяциях простейших (в разработке соответствующей математической модели принимал участие А.А. Витт). Методами, сходными с разработанными Вольтеррой, были проанализированы также модели симбиоза, паразитизма, конкурентных отношений между видами, использующими одинаковую пищу и т. д.
В последнее время в Новосибирске выполнен важный цикл работ по моделированию биогеоценозов (И.А. Полетаев, 1966; и др.) В них учитываются не только взаимодействие организмов, но и их отношения с неорганической средой (учет потока солнечной энергии, запаса питательных веществ в почве). Для многих модельных биоценозов вольтерровские уравнения не имеют устойчивых решений, в то время как природные ценозы отличаются устойчивостью на протяжении длительных отрезков времени. Работы, выполненные группой новосибирских исследователей, показали, что модели, в которых учитывается роль неорганических факторов, как правило, обладают устойчивыми решениями. И.А. Полетаев, кроме того, исследовал модели, в которых принималась во внимание сезонность поведения животных. Кинетика таких ценозов описывается дифференциальными уравнениями, коэффициенты которых в некоторые моменты дискретно изменяются.
В экологических моделях взаимодействующие виды считаются генетически однородными. В моделях генетики популяций, напротив, как правило, не учитываются экологические факторы. В настоящее время назрела необходимость совместного рассмотрения этих факторов, что делает создание математической теории эволюции видов и биоценозов крайне сложной, но зато и очень увлекательной проблемой.
* * *
Рассмотренные примеры проникновения математических методов и математического метода мышления вообще в различные области биологических исследований показывают, что этот процесс, начавшийся в конце XIX в., интенсивно продолжается и еще весьма далек от завершения.
Большинство перечисленных направлений и исследований по существу являются лишь первыми шагами и, по-видимому, отражают лишь основные тенденции процесса прогрессирующей математизации биологии.
Более 800 000 книг и аудиокниг! 📚
Получи 2 месяца Литрес Подписки в подарок и наслаждайся неограниченным чтением
ПОЛУЧИТЬ ПОДАРОК